Introduction to Io 41: Being = Space × Action: Searches for Freedom of Mind Through Mathematics, Art, and Mysticism

A consistent concern throughout the seminar was the study, interpretation, and translation of Parmenides. The seminar culminated with a public lecture given by Hennix on “Eleatic Set Theory,” which I introduced with an earlier version of the translation printed at the end of this issue.

Parmenides is usually recognized as the beginning of the “rational” tradition in Western philosophy. He is the first to leave a text behind in which the assertions are supported by definite arguments, and where belief demands proof.

Yet the Parmenides that appears in his fragmentary poem is not simply a rationalist in any familiar modern sense. He writes, for one thing, in verse, not prose. The occasion for his setting forth his arguments is a visionary journey; his mouthpiece, a goddess; and the object of his vision, an enigmatic and mysterious totality that, though unnamed, is referred to by the locution “esti” (it is) or “on’’ (Being). The Goddess who speaks of Being is Dike or Justice, and thus though the technical philosophy is thoroughly abstract in content, its domain seems to be the whole of human action, and its attitude, ethical. The Parmenides poem in fact opens a rather impressively large range of philosophical issues which remain unresolved to this day: the questions of the unity of knowledge, the unity of being, the unity of knowledge and being, the nature of proof, the nature of thought itself, the nature of justice, the relations between thought, proof, knowledge, and justice, the possibility of rational cosmology and the relationship between logic and cosmology, the existence and nature of abstract entities, the privileged status of philosophical knowledge—all these questions became explicitly formutable questions immediately following the production of Parmenides’s poem, none of them are definitely resolved today, and the future of science, culture, and the human spirit all depend to a far from trivial degree on how these questions come to be reflected upon.

But Parmenides was a visionary and a poet as well as a philosopher and mathematician, and as we were a group of poets concerned with philosophy, mathematics, and visionary matters, we took the task of discussing, interpreting, and translating Parmenides as an appropriate collective concern. The text of the poem comes to us in fragments recorded by later philosophers: Aristotle and Simplicius, principally. It is generally assumed that it appeared in two parts: one delineating a “true” path, the other, a representation of a path of mere opinion. The reason for this division is not clear from a study of the existing fragments. Numerous analyses have been suggested. It is also uncertain what proportion of the entire poem we are in possession of, and, in the case of certain passages, to which section they belong.

The poem is written in dactylic hexameters, the meter of the Homeric poems and the Delphic oracular responses; however, the diction is not derived from the Homeric dialect and if the formulaic theory of the technique of Homeric poetry is correct, the Parmenidean poem does not employ it. Exactly why Parmenides wrote in hexameters when there was already precedent for philosophers to write without them is conjecture.

Though the thought of the poem is supported by argumentation, this thought manifests in the context of an ecstatic vision. Parmenides is taken on a journey in a chariot, and with the assistance of the daughters of the sun god, he ascends into a super-celestial region normally forbidden to mortal inspection. Parmenides’s personal qualifications for the journey combine with a certain good fortune to create the conditions for his welcome by the goddess.

Parmenides’ chariot journey resonates with similar voyages occurring in the texts of cultures geographically proximate to and contemporary with the Classical Greeks, cultures whose interrelation with the Hellenic world is speculative but by no means impossible. I am thinking, in particular, of the Vision of the Chariot in Ezekiel and the metaphor of the chariot in the Upanishads. A variant of the image of the chariot as a metaphor for a spiritual journey is taken up, of course, in Plato’s Phaedrus. 

Parmenides tells us that the horses that drive his chariot have the capacity to take him as far as he wishes to travel. I read the horses as images for his own mental capacities, the chariot as the vehicle of thought cum contemplation upon which he journeys. Parmenides has mastered his own intelligence and his own mind as far as that is possible, and this qualifies him for contact with a transcendent source of wisdom, the goddess herself.

The goddess herself is unique to Parmenides. I speculate that the reverence paid to the goddess justifies the use of Heroic verse. In any case the hexameters do not appear to be wielded ironically: Parmenides is not mocking the poetic tradition by using its style. Though his thought is a new vision of reality and a radical critique of ancestral myth and recent philosophy alike, something of the sense of the sacred as manifested in the poetic tradition is being honored and carried forward here. Again, though Parmenides radically decomposes previous thought, the sacred awe of the truth that such predecessor ontologies radiated in their poetries is being transmitted in a new mode.

The symbolism of the poem is a species of mystical allegory wherein persons and objects, though figurative, cannot be replaced by the abstractions for which in fact they stand. Dike is more than abstract “Justice,” yet she is also more than an anthropomorphic goddess: Parmenides’s conversation with her and the instruction he receives from her constitute a communication and instruction from Justice itself; and Justice is taken as somehow identical with the transcendent object, the It Is, of which the goddess speaks. That Dike speaks in arguments and proofs bespeaks the nature of Justice: Justice is inseparable from correct reasoning, and the rationality of Being conjoins its own theodicy.

The restrictions on reasoning that Justice demands are stringent. In particular, a certain form of negative reasoning or negative existence is radically forbidden. That which Is Not cannot be asserted To Be, and thus no creature made up partly of Being and partly of Non-Being can be granted any share in existence at all. Being is whole, self-identical, bounded, invisible, eternal. It is like a “well-rounded sphere.” 

It has often been wondered how Parmenides could have permitted himself numerous negative expressions in the delineation of Being, if the existence of non-Being is to be so severely interdicted. But a recent study by Scott Austin demonstrates that the ban on negative language is itself limited to a ban on the positive assertion of negative subjects: such constructions as “the non-existence of X exists.”1 It does not disallow such assertions as “X does not have property Y.” Austin argues that Parmenides’s language is consistently disciplined in this way, so that the charge of self-contradiction or verbal unconsciousness will not hold.

The image of the “well-rounded” sphere is extraordinary. It has often been taken literally, as if Parmenides meant to project a spherical cosmology of a material sort. In fact, the image is clearly a simile—it is meant to express the concept that mensurable distances (such as the distances measured by geometers) have no application within Being. There is no distance as far as things of the mind are concerned. The aspect of the sphere that is intended in the simile is that which is contained in its formal definition: that all points on its surface are equidistant from its center. Similarly, all “points” or thoughts within Being are correlated without subdivision or hierarchical organization of any kind.

Parmenides’s “sphere of being” is often, in recent literature, taken as the prototype of the kind of systematizing, totalizing cosmologies and philosophies which, imposing themselves on the world, justify hierarchically-organized social structures, mind-stunning supersystems, and all the political, social, and theological tyrannies of Western history. But it seems to me it is important to notice that whatever the aspirations of systematic thinkers in the west from Plato through Hegel and Marx to Carnap and Goodman may be, none of them in fact takes up the challenge of the restrictions upon intellectual assertion leveled by the goddess. Plato (who is most often taken to be Parmenides’s heir) after explicitly merging the concept of Being and non-Being to form the hybrid Becoming, throws up his hands in despair of ever understanding what the Master really meant. The cosmological sphere of Being that Plato presents in the Timaeus, and which is generally thought to stem from Parmenides, is in fact a version of the sphere that Parmenides describes in the second part of his poem—the part presumably dedicated to a presentation of the way of “opinion,” namely—a “likely construction,” an “eikos logos.” But whereas for Plato such constructions are things one proposes when one has a hint of the truth but cannot prove it, precisely such hints and propositions are, by Parmenides, interdicted. 

Parmenides, then, far from being the progenitor of the totalizations and hierarchies of subsequent Western thought, and thus the figure most to be assailed at a time in history Western thought is tottering, stands outside of the whole tradition as a monstrance and a castigation against it, out of its origin. Parmenides was a hope that has not yet been fulfilled because his actual proposition has never been seriously entertained or analyzed with any particular depth.

The connection between the Parmenides poem and the cultures of India has been remarked upon. Something like Parmenides’s sphere of Being exists as a symbol for the Buddhist’s principle of the Dharmakaya; the expression of the absolute object of contemplation through the denial of a series of predicates is a common feature of Indian absolutism. Ingenious analyses have been offered likening Parmenides’s chariot journey—with its axle that gives off musical tones and radiates heat and light—to the processes of Kundalini Yoga. That Parmenides was educated as a Pythagorean is part of the Parmenides tradition. That Pythagoras’s doctrine, with its vegetarianism, metempsychosis, and general soteriological scheme owes its similarity to Indian metaphysics to Pythagoras’ personal journeys to the east is part of the Pythagorean tradition. Thus the possibility exists that the Parmenides poem reflects a hidden dimension of cross-cultural fertilization between India and the Ancient Mediterranean.

Another aspect of the Parmenides poem that looks suspiciously like typically Indian approaches to epistemology is its bipartite structure: the poem contains a doctrine of “two-truths,” one pointing towards an absolute that cannot be expressed properly in speech but can be acceded to through direct realization, the other a relative, conventional truth—a matter of historical convenience, common sense, or heuristic practice. The doctrine of two-truths is prominent in both Buddhist and Hindu metaphysics. Whether or not Parmenides’s poem owes anything to the east in this regard, the division of the poem into two contradictory doctrines deserves comment. A text that argues elaborately for the connection with India and which we discussed in Rhinebeck is Oscar Marcel Hinze’s Tantra Vidya (1979). I will reserve my own remarks on this topic for the supplement to this issue of Io where there will be further material dealing with Parmenidean questions.

My translation of the Parmenides poem provides a few readings but I was mostly concerned to take the text seriously rhetorically as a poem intended to celebrate the goddess Dike. Once again, I reserve comment on specific interpretive aspects of the translation for a supplement to this issue of Io.
Translation of course implies interpretation, and the question of interpretation/translation was an important aspect of the entire Rhinebeck enterprise. Quasha’s poems to some extent “translate” the states of cognitivity internal to their own composition, as well as interact in concrete and subversive ways with their “interpretative” machinery and habits of their readers. Hennix’s texts “translates/interprets” texts from the logico-mathematical tradition—Frege, Wittgenstein, Brouwer—in part by inserting them in a series which includes Parmenides on the one hand and the Japanese Hekigan Roku on the other.

• 1Parmenides, Being, Bounds and Logic (New Haven: Yale University Press, 1986)

After Parmenides, a second personage studied by us in Rhinebeck was the modern Dutch mathematician L.E.J. Brouwer. Brouwer is the founder of the Intuitionist School of Foundations of Mathematics. He was himself a contemplative and a mystic, and the inspiration and motivation for his mathematical work remained throughout his career inseparable from his spiritual concerns. Brouwer is a major influence on modern mathematical theory, both behind the scenes and center stage, though his work is not frequently studied today in academic circles even where intuitionism of a certain type is in favor. He is, however, a major influence on both A.S. Yessenin-Volpin and Catherine Christer Hennix. The appendix to this introduction includes several of the key passages from Brouwer’s work that express his views on the contemplative life. I will attempt, in due course, a conjecture as to the connection between mathematics and contemplation his work suggests.

In order to see Brouwer’s position in mathematical thought, it is necessary to grasp how the intuitionist school compares in outlook with other mathematical philosophies. I will sketch these views very briefly, and refer the reader to the introduction and opening selections in the anthology of essays edited by Paul Benacerraf and Hilary Putnam, Philosophy of Mathematics, Selected readings, for further discussion.1

It is often remarked that there have been three distinct approaches to the question of the ontological status of mathematical objects in modern times:

1 classicism (or Platonism)

2 formalism (or conventionalism)

3 intuitionism (or constructivism)

with constructionism playing a part in formalism.

For the classicist or Platonist, mathematical objects are objectively-existing entities. The mathematician discovers these entities and studies their properties in a manner analogous to the way a natural scientist discovers and studies natural phenomena. Thus, the intellectual activities involved in developing mathematical systems are extrinsic to the systems themselves. Natural numbers, ideal geometrical objects, axiomatic structures—in short, mathematical entities in general—are considered to be existences independent of the thinking mathematician. Mathematical language expresses but does not determine mathematical truths, and the entire mathematical universe is conceived to be a hierarchy with logic and set theory at the apex.

In contrast, for the formalist, mathematical objects are purely conventional. They consist solely of written marks and the rules devised by persons for the manipulation of those marks. Mathematical systems have no ontological significance apart from the ontology implied in their being concrete inscriptions of signs. Whereas for the classicist a proof is a demonstration that certain objects exist in an ideal mathematical cosmos, for the formalist a proof is simply an algorithm: a strict procedure for deriving strings of symbols from other strings according to perfectly explicit rules. Any relationship to “reality” that such systems may possess derives from interpretations or “models” of those systems: ways of associating certain strings of symbols with physical or other realities. The intellectual activities involved in developing mathematical systems are perfectly extrinsic to the systems themselves, except in the sense that the activity of devising the rules of procedure is an intellectual activity. The rules once devised, however, can be executed perfectly well by a computing device without reference to human intervention. Mathematical language (the marks and the rules for use) constitutes the whole of mathematics.

For the intuitionist, mathematical objects are constructions of the human intellect: the “creating” or “creative” subject, to use a phrase coined by Brouwer. A mathematical object is intrinsic to the intellectual activity involved in thinking it. It is neither true by convention, nor is it a feature of the objective universe. In fact, in its most radical formulations, both the objective universe and the world of human convention are themselves derivative of the mathematical activity of thinking subjects. A mathematical object becomes real by its being thought, by its being constructed concretely in the mind of a thinking mathematician. 

While classicism is in a sense derived from Platonic philosophy’s emphasis on the reality of abstract ideas, its modern developments are due more to the mathematicians of the Renaissance and finally to Descartes than to the notions of the Greeks. (For an excellent account of the development of Renaissance mathematics and how it differs from that of the properly classical period, see Jacob Klein’s Greek Mathematics and The Rise of Modern Algebra and Don Byrd’s essay in this issue.)

Modern formalism is associated mainly with David Hilbert. Intuitionism derives ultimately from Kant’s apriorism, but gets its major impetus from Brouwer. Brouwer’s approach to mathematics was based, as we have noted, upon a perspective that was decidedly “mystical” or “contemplative” in origin. Brower’s PhD thesis, Over de Grondslagen der Wiskunde (On the Foundations of Mathematics, 1907), in which many of his major mathematical notions receive their initial formations, was composed simultaneously with his Life, Art, and Mysticism (1905). The two texts were intended to complement each other, though his thesis advisor forced him to remove the passages from his thesis which would have provided the links between them. Brouwer never retracted his mystical views, however embarrassing they proved to his tutors and subsequently to his disciples.

Brouwer’s intuitionism begins with a severe critique of classical mathematics on numerous points—points which were later taken up by Hilbert and his followers and incorporated in the conventionalist program. Later too, Brouwer’s intuitionistic reconstruction of mathematics was rewritten by his disciples without grounding the system upon the fundamental intuitionistic acts that had been their origin. In other words, much of what is presently called “intuitionism,” though derived indeed from Brouwer’s alternative methods for constructing mathematics, is intuitionism in name alone in that it does not seriously depend upon the concrete acts of intuition in the mathematical thinker’s mind.

Brouwer viewed mathematics as being built up from certain profoundly private internal acts of the thinking psyche. These acts take place in the loneliness of the thinker’s internal life and constitute the inner gestures performed between the self and its deity. Mathematical intuition is thus fundamentally independent of language—independent even of the disambiguated language of mathematical thought—and profoundly removed from the language of the everyday. Mathematical language functions to help the thinker remember his thoughts or to aid in the stimulation of such thoughts in others, but is finally inessential to the nature of mathematical truth itself.

The controversy between the three main schools of mathematical thought of course touches many philosophical topics, but let me confine myself to the following two:

 

1 the question of the ontological validity of natural science

 

2 the link between intuitionistic thought and contemplative modes of enlightenment.

Natural science aspires to validations through a certain hierarchical organization. The social sciences and “sciences of man” must depend upon the biological facts pertaining to the human species as discovered by biologists. Biology in turn grounds its analyses of biological phenomena upon the chemical substrate of those phenomena; and chemistry has achieved “certainty” through its dependence on quantum physics. Physics is the ideal and basis for all natural science in that its findings are expressed in precise mathematical language. Indeed, the truth claims of the physicist are really limited to the formulae and equations which depict the regularities discovered in the experimental data. Thus, if physics possesses determinate ontological content, that content both determines the ontology of the other sciences and rests upon the ontological import (or lack thereof) of the mathematical language in which it is expressed.

Of course, this view of things is over-simplified and not without its challengers, and would need much qualification to be made precise—there are numerous biological and sociological concepts which are not derived from the position in the above hierarchy: concepts of structure, function, pattern, etc. But all such concepts apply to physical systems which in turn have their analyses on the next hierarchical level. If the independent concepts are to be given ontological significance without recourse to this founding level, the entire edifice of physical science loses its coherence, and ontological principles outside of physical science must be sought to ground these structures. Again, certain phenomenologists argue that the hierarchy sketched above itself grows as “regional ontologies” or as derivative structures from more primitive domains. But in such cases the ontological significance of science is sought outside of the domain of science. The point here is simply that if the edifice of science as a whole demands recognition as positive knowledge, then it must be able to provide its own ontology. In any case the ontological significance attached to the mathematical language in which the base of the system is expressed will determine just what the ontological significance of the sciences are. It will be argued by some that, presently, science proceeds not as an organized hierarchy of disciplines, but as a multiplicity of heterogeneous activities with various relations to each other and to the world. But this condition of incoherent multiplicity follows from the abandonment of ontological finality as a desideratum, a consequence of precisely the formalist philosophy. At the very least what can be said is that the current state of things rests upon a philosophical outlook which itself is far from unanimously defended.

In any case, the ontology (or lack thereof) of natural science depends upon the nature of the “truth” inherent in mathematical language, or the nature of mathematical validity itself. If there is NO CONSENSUS on the nature of mathematical language, any consensus the physicists arrive at regarding their own theories must be considered indecisive. The many assertions that the ontological meaning of the physicists’ theories can well remain indeterminate (since it is the pragmatic, i.e. technological, efficacy of these theories that really backs up their truth claims) are all well and good IF one is willing to admit the reduction of all science, including theoretical physics, to the province of technology. This admission would entail that there is no “pure” science at all, and that to look to science for anything more than technical means for attaining practical ends must be renounced.

We turn now to a discussion of the link between intuitionistic philosophy and contemplative concerns.

We will see the intuitionist in two quite distinct though related attitudes. One of these is in fact not incompatible with at least certain formalist-constructivist possibilities and has a reasonable number of adherents (including, in a sense, Yessenin-Volpin, though Yessenin-Volpin goes much further than other formal-intuitionists in emphasizing the concrete realization of construction methods. Also, Yessenin-Volpin’s work is ontologically anarchic rather than, as is the case with formalism, indifferent). The second attitude, though clearly the attitude of Brouwer himself, has few vocal adherents in the mathematical community. Let us call the first attitude formal intuitionism and the second intuitionism proper. Formal intuitionism and intuitionism proper do not differ necessarily in their propositional content, but rather in their ontological stance. Thus, I will sketch first formal intuitionism, and what I say here can be assumed to hold for intuition proper as well, though not conversely.

Formal intuitionism coincides with classical mathematics when dealing with finite mathematical objects. But the main developments of modern mathematics have explored the rich domain of infinite or “transfinite” magnitudes and orderings, so the coincidence is in fact relatively trivial. Formal intuitionism denies the law of the excluded middle for infinitary systems. And this denial does not refer in particular to the demand that the value “undecidable” be admitted as an alternative. In classical mathematics, a proposition is undecidable or unsolvable if the application of the procedures of the system yields NEITHER the values “true” nor “false” when carried out. Such propositions are said to be independent of the formal system chosen and they may therefore serve as axioms. Hence, the Russell Paradox in naive set theory can be considered undecidable, and in certain interpretations of the “Liar Paradox” the liar-statement is judged to be undecidable. But for the intuitionist, since an object cannot be said to exist until it has been constructed, nor can it be denied that it might exist until it has been shown that it cannot be constructed—there will be objects whose existence can neither be affirmed nor denied. These objects will also not necessarily lead to paradoxes. The point is not that the existence of such objects cannot be decided formally, but rather that their existence HAS NOT YET been determined. Time distinctions thus become an important part of intuitionist thinking, especially in the system of Yessenin-Volpin.

A frequently cited example:

Consider the decimal expansion of π. A procedure has long been known for indefinitely extending the sequence of digits defining the value of this irrational number. Today, this procedure is being carried out to ever-further decimal places by computers, so that progressively the value of π will grow more and more lengthy and more and more “precise.” Now consider some arbitrary sequence of digits (a,b,c, . . . n) that has not as yet turned up as a particular segment of the sequence of digits constituting the decimal expansion of π. We ask whether the proposition:

P.1.“(a,b,c, . . . n) belongs to the decimal expansion of π”

is true or false? According to a classicist, this question has a unique answer that already exists: it just hasn’t been discovered yet. But the intuitionist points out that, although as soon as (a,b,c, . . . n) has been found, the value “true” (or not false) can be assigned to the proposition, since the expansion of π does not terminate, the procedure could be applied indefinitely without our having a proof that P.1. is either true or false. There will never come a time when we will have generated a sufficiently long enough decimal expansion to decide the question negatively. The intuitionist therefore argues that the answer to our question does not at the present time exist and that the classical position has been refuted. We cannot know anything about the properties of such a sequence until we actually construct it.

The example of a decimal expansion of π is not trivial. The question it raises infects the entire question of the “existence” of irrational numbers (which are understood as non-repeating non-terminating decimals) and through these to the understanding of the structure of the mathematical continuum, i.e. points laid out on the “real line.” For Brouwer, the continuum is not a unique concept with eternal properties to be established once and for all. Its nature varies with both the specific details of its construction and the precise degree to which procedures of its construction, at a given point in time, have been carried out.

Formal intuitionism thus amounts to a restriction on logical rules when applied to infinite objects. As such, it can be taken over whole cloth and given a formalist interpretation. Such in fact was carried out by students of Brouwer; and, today, when logic itself has been generalized within category theory, intuitionistic logic, and intuitionistic set theory appear as formal variants of mathematical structures, as legitimate within logic as non-Euclidean geometries are within modern geometry.

But what is the relationship between formal intuitionism and intuitionism proper—intuitionism as invented and presumably practiced by Brouwer? And how does this relationship bear on the possibility of a rapprochement between mathematical thought and contemplative consciousness?

Brouwer’s intuitionist mathematics cuts down severely on the universes (species) of mathematical objects. The motivation for doing this was to provide a foundation for mathematics. In prosecution of this aim, intuitionism is in competition with the project initiated by Frege, watered down by Russell and Whitehead, and brought to a head by Hilbert and his school (including the young Gödel), to reduce all of mathematics to afinitary structure such as, for example, a finite set of axioms. Frege had actually proceeded along intuitionistic lines, identifying logical norms with general principles which can be effectively carried out (though he is commonly thought to belong to the classical camp); Hilbert, working formalistically, also viewed logic with a constructive interpretation where, in particular, the concept of decidability was emphasized: you stipulate the rules of logic explicitly so that they can appear as algorithms. But the goal of Hilbert’s project was to reduce all of mathematics to a finitary system called metamathematics (or proof-theory) and, as a by-product, to obtain a consistency proof for classical arithmetic by the use of logical principles even more restricted than Brouwer’s! In fact, this is precisely Hilbert’s “second problem.” In contrast to both of these, Brouwer thought all intellectual activities carried out by means of notational systems (whether those systems are derived from ordinary language as in philosophy or inscribed in the rarified notation of the formal logic of Russell, Whitehead, et al.)—that all intellectual disciplines of this sort—are in fact initiated by human conventions for human convenience. Mathematics, however, is based on fundamental and inalienable intuitions that precede all logical or linguistic norms. The foundations of mathematics are not to be sought in the logic of formal systems at all. Mathematics is to be founded by linking it to fundamental intuitions of thought-processes of the thinking subject. Moreover, these intuitions of thought-processes are at the basis not only of mathematical thinking, but of consciousness itself. Brouwer’s speculation founds mathematics upon specific modes of human intuition, while at the same time finds human consciousness itself to be a form of mathematics (mathematics being understood precisely in the intuitionistic sense).

The fundamental intuition that grounds both human consciousness and mathematics, Brouwer calls the awareness of “a move of time.” A move of time is a minimal element of consciousness. It is similar in nature to the notion of a “point-instant” (familiar from occasionalist thought in its various forms—Islamic, Jewish, Buddhist, Cartesian, Whiteheadian, Russellian, etc.), i.e., the notion that time (and the material objects, or moments of awareness within time) consists of a linear continuum of point-like moments of infinitesimal duration, which vanish as they arise and are replaced spontaneously by successor moments. This concept of time, however, abstracts from dynamic temporal experience and reduces the enigmas of temporality to the problem of the linear continuum. For Brouwer, the linear continuum itself is to be built up from the experience of time, so such a reduction is impossible. What is required is that certain fundamental properties of the continuum (for instance, that neither temporal continuity nor discreteness are derived from each other) must already be present in the temporal experience from which they are extrapolated. Brouwer accomplishes this by asserting that the fundamental element of temporal consciousness already has an irreducibly complex structure; it is not a point-instant, an indivisible, durationless unity, but a “twoity”—a dyad with the following characteristic: each moment of consciousness spontaneously splits into two parts: 1, the trace of itself surviving as a spontaneous memory; 2, the succeeding moment. This new moment repeats the process, similarly splitting into the trace of itself and its own successor. Both the dynamic character of time and the way consciousness is bound up with temporality are thus built into the fundamental concept. The duality, continuity/discreteness, is also established thus at the foundation.

The discovery of the twoity as the fundamental entity is to be an act the thinking subject must perform for itself. It involves a deliberate concentration of consciousness on its own streaming, and a concrete wrestling of this fundamental abstract structural core. The twoity and the succession of twoities are to be discerned as the “empty” substratum for all experience by an act of self-intervention that the reader may feel, as I do, is profoundly connected to the act of “turning into oneself” that Brouwer recommends in Life, Art, and Mysticism (see Appendix II). Brouwer does not explicitly draw this connection, but whether or not his mystical speculation will be experienced as relevant to his mathematical thinking depends upon our providing that link. Indeed, whether or not his demand for the restriction of the use of the law of the excluded middle can be connected to his founding of mathematics on radical temporal experience may depend entirely upon whether or not one undergoes that radical temporal experience. In any case, from the procession of empty twoities, one proceeds to develop the elementary series of mathematical thought.

Now the procession of twoities when it becomes explicit for consciousness founds the construction of the conscious intellect, yet at the same time, the procession of twoities itself is inherent in the subject. It is through processes directly analogous to the development of explicit mathematical thinking that consciousness builds up a world. The link between mathematical thinking and the development of consciousness (what Hennix will call attention to as the link between semeiosis and cosmosis) is the notion of a series. Consciousness experiences two species of series: one it discovered as causally-related temporal sequences, the other it constructs into things—objects with durative identity. A causal sequence requires that the order relationship among the members of the series be preserved, while an object is coalesced from a series of impressions whose members may be considered independently of their position in that series. Brouwer writes in “Conscious, Philosophy and Mathematics”:

An iterative complex of sensations, whose elements have an invariable order of succession in time, whilst if one of its elements occurs, all following elements are expected to occur likewise, in the right order of succession, is called a causal sequence.

On the other hand there are iterative complexes of sensations whose elements are permutable in points of time. Some of them are completely estranged from the subject. They are called things.2  

Our belief that event X is the cause of subsequent Y, which in turn is the cause of a third event Z, depends upon the temporal order of X, Y, and Z. If Z precedes X, it normally cannot be the cause of it. But the sequence of momentary impressions of an object O can be recalled in any order we choose without disturbing our belief that the object O is the same entity, perduring throughout its various momentary appearances. Causality and thinghood are thus both brought under the single concept of a series, and the latter concept is derived from a fundamental intuition of time. The world is built up by the soul as a complex concatenation of both kinds of such series.

At this point I refer the reader to the passages from Brouwer’s work included as an appendix to this introduction. These passages bear upon the notion of the sequences of twoities and the relation between Brouwer’s intuitionism and his mysticism. First, Brouwer’s statement of “The Two Acts of Intuitionism” (Appendix I). These passages were repeated in subsequent works and stand as the founding statements of intuitionist thought. They will be followed by excerpts from Life, Art, and Mysticism. Both sets are presented as selected by Hennix and published as excerpts in his text Brouwer’s Lattice. Brouwer’s Lattice was “required reading “ at the seminars and the excerpts represent what Hennix wished to present to us of Brouwer’s mystical thought.

• 1 Benacerraf and Putnam, Philosophy of Mathematics, 2nd edition. (Cambridge: Cambridge University Press, 1983).
• 2Brouwer, Collected Works, Vol. I (Amsterdam: North-Holland, 1975), 1235.

There have been very few commentators, besides Hennix, on the connection between Brouwer’s contemplative and mathematical views. It has seemed difficult to many to see how Brouwer on the one hand derives arithmetical systems from his twoities, and how, on the other hand, the system derived from twoities and series of twoities links to his mystical ideas.

If the serious business of the soul involves a turning into the self and a turning away from “the Sad World” of constructed, willful, public reality, as Brouwer maintains in Life, Art, and Mysticism, how can the creation of a mathematical universe facilitate this “turning into the self”?

Tentatively we can conjecture that Brouwer’s construction of mathematics provides him with the possibility of exhausting the activity of his own intellect in a way that liberates him from the cunning and deceit of “the Sad World.” Brouwer’s intuitionism provides, at every step, links back to the “Creative Subject’s” own activity in constructing the cosmos and provides a system of procedures which makes it possible for anyone whose motivations are congruent with his own to retrace the path of humanity’s intellectual catastrophe (as outlined in the excerpts given in our appendix), and, at the same time, to avoid both the absolutism of classical mathematics and the nihilism of the formalist school.

I will develop this conjecture by considering how Brouwer escapes from the deceptive consequences of the concatenation of the Sad World. (I use Brouwer’s phrase “the Sad World” to refer to the world of human experience and culture as built up from serial concatenations.) This will involve first of all an interpretation of how both arithmetic and consciousness are derived from the series of twoities.

The generation of the twoities in Brouwer’s system can be interpreted as developing along a pair of axes: the reiterated series of empty twoities proceed concretely in time along a horizontal axis; processes of intellectually constructing further series of twoities (or multiplicities of series of twoities) occur along the vertical axis.

The horizontal series of twoities, developing in time, constitutes a concrete experience of emptiness—a fundamental experience of time to which the Creative Subject returns ad libitum, as a way of “emptying out” its consciousness, at any point in the process of construction. The series of empty twoities forms a fixed series, a bottom line to which consciousness is always free to return. It is the basis of all constructed existence, the reiterable fundamental intuition grounding and regrounding both thought and the world grasped by perception and thought. At every moment it is independent of all concrete content, yet, because it is wedded to a specifically subjective experience of time itself, it is the most concrete of things.

The vertical series of constructions represents successive generations of indices for chains of positive cognitive acts, perceptions, and mathematical constructions. The complexity of our world and of our thought, and our bewilderment before both—all derive from the interplay of these vertical constructions proceeding in forgetfulness of their purely derivative character.

The vertical axis is built up as follows:

Arising from any twoity along the horizontal axis, conceive a series of abstract constructions. At the position immediately above any selected twoity, find a conceptual copy of that twoity together with a copy of the two unities of which the original twoity is composed.

These two unities, it will be remembered, represent a pure moment of sentience (divested of all content) which has spontaneously split into a successor moment and a trace of itself. The abstract copy of the original twoity together with the copy of the two unities constitutes a new twoity: a new bi-unity, an abstract representation of the original pair of unities of which the original twoity was composed, and the conceptual combination of these two unities into a new bi-unity. This process can now be iterated, each new abstract twoity being composed of the two prior unities together with their unification into a new unity, constituting once again a new bi-unity. Each successive iteration of this process grows more complex, in the sense that the content of each consists of larger and larger complexes of twoities and unities. And the series of ever greater complexes of twoities and unities will be able to serve as an index for ordering other sequences of objects, perceptions, or constructions. The series of twoities, ever growing in complexity, serves as a construction of a natural number series or even the continuum of real numbers itself.

While the horizontal series takes place in the concrete real time of the Creative Subject, with each twoity existing only in its own moment and surviving only as its own trace in the successor twoity, the vertical series generates an atemporal conceptual space, in which each successive abstract twoity enjoys a kind of hallucinatory pseudo-existence.

Each successive stage in the development of the “vertical” series must take place within the real-time existence of the creative subject, yet it is precisely the property of this ascending series of abstractions to neglect this temporal character, and to generate a symbolic space in which predecessor twoities continue to exist as successor twoities are formulated.

Though we have been referring to the original succession of horizontal twoities as a series, as a matter of fact, the possibility of anything existing in series only emerges with the vertical series. The horizontally-extending emergings of twoities perpetually perishes, leaving only its traces in successor twoities. It only becomes possible to identify the horizontally emerging twoities as a series after we have indices for them. And this becomes possible through the fact that the ordering of the vertical series can serve as a system of indices. (The possibility of the construction of the vertical series, however, derives from the fact that the horizontally-extending twoities have a dyadic structure: the individual point-moments of temporal consciousness are in fact bi-unitary, for it is only by abstracting from the possibility of trace of a predecessor moment that an abstract series of ascending twoities can be formed.)

The vertical series of twoities can, as we mentioned, be treated as a natural number series: a set of indices whereby other series of otherwise absolutely transitory phenomena in the experience of the Creative Subject can be linked to a conceptual space which enjoys quasi-independence from the uncompromised evanescence of the temporal domain. Thus, the two species of series (which Brouwer identifies with objects and causal sequences) are concatenated by consciousness by linking them to members in the vertical series of twoities which, in the form of natural number series, serve as indices for their members.

The existence of both objects and causal sequences are capable of being cognized by the Creative Subject because they can be indexed by the members of the vertical series of twoities.

But because the entire vertical series of twoities has no concrete existence, the Creative Subject is at every point of its existence free to “drop down,” as it were, to the horizontal axis and recover the emptiness of its own actual condition. The vertical series of twoities (and the causal and objective series for which it serves as an index) only exists as long as a concrete Creative Subject sustains it and no longer. The entire construction of the Sad World is thus seen as being at every point capable of being collapsed back into the empty but concrete continuum of the creative subject’s only authentic life.

This possibility of “dropping down” to the horizontal axis at any point in its life allows the Creative Subject to remain free from ensnarement by the construction of intellect and consciousness, free at every moment to resume its silent communion with its spiritual ground.

In Hennix’s work, the concept of the Creative Subject, taken over from Brouwer, together with the bi-axial construction, gets explicit development. In her “Theory of the Creative Subject,” the atomic conceptual acts called “noemas” correspond to Brouwer’s series of temporal twoities, while the vertically-rising series of denotational connections correspond to Brouwer’s vertical axis of intellectually constructed twoities. But before looking at Hennix’s work we need to sketch some of the main ideas of Yessenin-Volpin. We will also look at two further topics of general interest that play key roles in Hennix’s thought: category theory and the procedure of diagonal substitution.

Alexander Sergevich Yessenin-Volpin is a Russian refugee who has recently become a naturalized American citizen and who presently lives in Boston. He is perhaps best known as a co-founder of the Soviet Human Rights Movement (together with Sakharov), but he is also the founder of “The Ultra-Intuitionist School in the Foundations of Mathematics.” An outline of the program for this school is contained in an article published in Kino, Myhill, Velsey: Intuitionism & Proof Theory (Amsterdam, 1970). Though it is far too subtle and intricate for me to summarize fully in these pages, I strongly recommend it to the readers of Io. It makes few demands upon the reader in terms of formal preparation, develops its own symbolism quite lucidly, and is thus a text which can be read by the interested novice.

To give a sense of who Yessenin-Volpin is as a human-rights activist, I quote here from a biographical, editorial introduction to an article by Yessenin-Volpin from The Humanist, January/February 1973. 

After many attempts to leave the Soviet Union failed, Aleksandr Yesenin-Volpin [sic], distinguished mathematical logician, was finally granted an exit visa in May of 1972 . . . 

Dr. Volpin had been a key figure in the democratic movement in the Soviet Union, and, as a result, he had been constantly harassed and intimidated by the government. During Stalin’s era, he was committed to a mental institution for writing two anti-Stalinist poems . . . After Stalin’s death he received a pardon. He edited the section on Mathematical Logic of the journal Mathematica . . . In 1959, he was invited to participate in an international symposium in Poland but was declined a visa. He was imprisoned in 1959 and put in a special mental hospital in Leningrad, but was released in 1961 . . .

On December 5, 1965 (Constitution Day) he participated in a demonstration on behalf of Siniavski and Daniel in Pushkin Plaza, Moscow, carrying a sign reading “RESPECT THE CONSTITUTION!” He was arrested, but released . . . In February, 1968, he applied for a visa to travel abroad. He was, for the fifth time, incarcerated in a mental institution. A letter of protest from 95 mathematicians and scientists helped to secure his release.

Yessenin-Volpin calls his program “an anti-traditional program,” and it is based upon a putting into doubt of at least eleven principle assumptions usually left unexamined in classical mathematics. Rigor in mathematics generally develops by making explicit assumptions which hitherto had been either concealed or taken for granted. Making such assumptions explicit may have the destructive but salutary effect of pointing out contradictions hidden in what had seemed to be a secure system. But such destructive discoveries most frequently lead to a deepening of mathematical understanding and the opening of fresh ground.

Groundbreaking criticism of this order, however, frequently meets with a two-fold resistance: first, the desire not to shake unnecessarily the foundations of systems and practices apparently in good use; second, the seeming self-evidence, triviality and harmlessness of the assumptions exposed. Novices in mathematics complain that much discussion in foundations amounts to quibbling over what seem to be pointless differences. Yet it is precisely at the level of seemingly unquestionable assertions that the structure of our unconscious cognitive commitments reveal themselves. For this reason, Yessenin-Volpin operates on the principle that everything should be open to question.

I will not be able to examine all the points that Yessenin-Volpin challenges, but will sketch out the implications of a few of them. First of all, he rejects the uniqueness of the system of natural numbers. The natural numbers are not a system of entities existing in a single form for all time. They must be constructed concretely for each context of use. And different constructions can be brought into comparison. Yessenin-Volpin shows that it is possible, for instance, to disagree about the nature of an infinite series of natural numbers: the classical concept of infinity holds that the natural numbers form a completed totality. Yet it is possible to hold that such a totality does not exist, i.e. that the natural numbers only extend as far as it is effectively possible to compute them. To give an informal example: a number such as 1012 to which no one has ever counted, since it is not a humanly (non-computer-aided) feasible number, can be defined as “playing the role” of an infinite number in a humanly-feasible substructure of arithmetic. Since it can be shown that it is possible to construct number systems according to these two different concepts of the meaning of the term “infinity,” it is thereby informally demonstrated that the natural numbers do not form a unique system, i.e. that axioms of limitation of size in arithmetic are independent from each other. Yessin-Volpin generalizes this idea presented as systems in which two (or more) number systems are employed concurrently, and specific rules for embedding one inside the other are established. (The uniqueness of the natural numbers is a main feature of the classical belief that mathematical entities are objective and independent of our constructions. The recognition of the plurality of number-systems actually is a return to a way of thinking about numbers which was current among the Greeks. See Jacob Klein’s Greek Mathematics and the Rise of Modem Algebra.)

Category theory is among the most abstract systems of mathematical thought that exist to date. The “categories” of category theory are themselves whole mathematical systems; thus, the sets in Zermelo-Frankel set-theory are objects in a category, topological spaces form a category, linear algebra is a category, group theory is a category (category theory generalizes the well-known concept of a semi-group with unity). In other words, category theory generalizes over and draws its concepts by abstracting from lower-order mathematical disciplines, much as traditional algebra generalizes over arithmetic or topology generalizes over geometry.

Category theory, however, reaches such a level of abstraction that even logical constants and most of the logical rules applicable in lower branches of mathematics are themselves susceptible to analyses and thus to variations. 

Though category theory generalizes over lower disciplines, it remains in its concepts and terms quite free of the disciplines it “categorizes.” It may more fruitfully be thought of as an independent body of concepts from which other disciplines can be derived, than as an abstractive generalization from those disciplines. 

Initially, the inventors of category theory hoped to provide a foundation for mathematics alternative to that provided by set theory, but that hope was disappointed because of the theory’s extremely high level of generalization. Eventually, Lawvere and Tierney elaborated the notion of a topos: a topos adds additional structure to the notion of a category and makes it appear to be suitable for the founding of mathematics. The topos concept, however, turned out to involve intuitionistic principles (formally intuitionistic principles, that is), so one had the rather paradoxical situation of being in possession of an intuitionistic theory of the foundations of classical mathematics. It is this circumstance upon which Hennix seizes in his work.

The entities with which category theory concerns itself are called “objects” and “morphisms.” An object may be anything at all conceived of as an object. Thus, the objects of a category might be sets or natural numbers or topological spaces but they might also be states of consciousness or ordinary items of the everyday world. The “morphisms,” which are generally indicated by arrows connecting the symbols or objects, stand for operations which are performed on, among, or between the objects. If the category is set-theory, for example, the objects would be the sets and the morphism, the set-functions such as membership, intersection, union, and the like.

In addition to possessing objects and morphisms, in order to qualify as a category, a system must enforce certain rules. Morphisms must be capable of “composition”: that is to say, a transitive relation between morphisms must obtain, such that the morphisms can be performed in sequence: if an arrow f connects an object A to an object B, and another arrow g connects object B to object C, there will always be a third arrow h called the composition of f with g connecting A to C. The diagram:

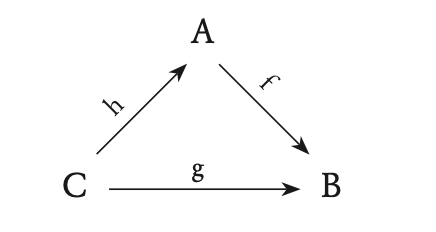
is called a “commutative” diagram and is used in category theory to render, in a compact and intuitively obvious notation, the relations between the objects and morphisms. The composition of arrows must be transitive except in the case of the “empty category”: the category which has no objects and no arrows. If a mathematical system does not exhibit transitivity, then it cannot be generated within category theory, i.e. an intransitive system is represented by the empty category.

In standard developments of category theory the empty category has little application. As most mathematical systems affirm transitivity, the empty category is developed within category theory mostly to complete the symbolism. Yet in Hennix’s use of category theory, it is precisely the empty or “almost empty” category that proves to be the richest and most rewarding of study, since his concern is frequently with intransitive structures—structures which thus occupy what she calls “the interior” of the empty category (interpreted as a set).

Since category theory deals with principles held in common by different systems, special processes are required to establish connections, transformations, and relations between different categories. Such processes are called “functors” and, like morphisms, are indicated by arrows, pointing now from category to category rather from object to object.

Among the morphisms that get particular attention in Hennix’s work are the “pushouts” and “pullbacks.” Pushouts may be viewed as arrows that indicate the generation of theorems from axioms within a category, while pullbacks may be viewed as indicating the reduction of the theorems to the axioms from which they have been generated. (These ideas come from algebraic geometry, in particular, sheaf-theory, and are expressed structurally as “Grothendieck topologies.”) A functor that gets special attention is the universal “forgetful” functor which eliminates levels of specification between categories. By a judicious use of pullbacks, forgetful functors, and the empty categories, Hennix is able to indicate structures which obtain for aesthetic and ascetic processes, usually thought to be incapable of logical presentation.

A topos, as we mentioned, is a category with certain important additional structural features. It was through the elaboration of the topos concept that, as stated above, Lawvere and Tierney were able to initiate the employment of category theory as a theory of the foundations of mathematics. Rather surprisingly, even the Environment E discussed extensively by Hennix below is a topos, or rather contains an unlimited “universe” of toposes.

Toposes contain methods for classifying and indexing the objects of the category, so that it becomes possible in a topos to symbolize a collection of objects, relations and operations together with a system of indices distinguishing and classifying those objects, relationships, and operations. It is this feature of the topos that makes it an appropriate structure for the study of the logics implicit in cosmologies, psychologies, and all disciplines where objects must be considered together with their modes of representation.

The Yellow Book1 deals throughout with constructions that are known in mathematical language as “diagonal” constructions. These constructions extend formal systems where the application of the operations of such systems to certain values leads to contradiction. A diagonal construction often becomes necessary, for instance, where systems encounter self-reference: if a function is taken as an argument for itself, the value of the function is either undefined (and the system is incomplete), or the system becomes notationally inconsistent (and the system is over-complete), or else the system must be expanded in some way to accommodate the self-referential case (making use, for instance, of fixed points in metamathematical extensions). The expansion of the system is obtained by first adjoining to it the operation of “diagonalization” and then picking any diagonal formula as a “new axiom.” A situation where diagonalization is exemplified usually occurs whenever a formal system is construed as taking arguments for ALL its values, then there will occur a case where the system will have to refer to itself. In general, where unrestricted self-reference is allowed, paradoxes arise.

Diagonal constructions occur in mathematics where the limits of a given notation are reached, yet where one insists on the possibility of continuing to apply the operations already defined in particular, iterated compositions of operations with themselves. Thus, the creation of fractions to indicate the ratios between whole numbers, the creation of irrationals to indicate roots of numbers not perfect squares, and the recursive development of multiplication from addition or exponentiation from multiplication are all instances of diagonalization. 

In modern mathematics, diagonalization plays an important role in the concept of the “transfinite” numbers of Cantor, and the battle over the legitimacy of the transfinite numbers rages over the interpretation of the diagonal procedure that produces them. Again, it is the “diagonal” case in Frege’s foundations of arithmetic, the existence of sets which can take themselves as members, that generates the paradox discovered by Russell which constitutes the central crisis in modern mathematical thought; and a very elaborate diagonal procedure is at the heart of Gödel’s famous incompleteness theorems. Finally, the entire issue of what is “unsayable” in Wittgenstein’s Tractatus Logico-Philosophicus hinges upon the diagonal construction which would have to be provided were the process of “picturing” allowed to picture itself.

There is a singular interest attachable to diagonal and self-referential constructions which has been frequently commented upon in both popular and serious mathematical literature, for self-referential situations do not only show up under formal conditions: they may appear wherever a symbolic system is in use, whether such a system is an ordinary language, a philosophical or technical discipline, a biological system of cognition or perception, a work of art, or a system of spiritual exercises. That is, in any system of representation where the free-variable terms of the system have been allowed to range over the totality of their domain, there will occur a diagonal case, a term which refers to the system itself. In each such system, the diagonal or self-referential case will have the appearance of singularity, a moment of confusion, an occasion for doubt, or else will seem a justification for the expansion of the system, for a mystical flight into transcendent realms—depending on the context of the system and the perspicacity of its devisor.

A few examples: the diagonal case in a psychological theory occurs when that theory attempts to account for how the psychology of the theorist affects the psychological theory being propounded (one thinks of C.G. Jung’s famous remark, “we do nothing but dream the myth onward” or the problem of transference and counter-transference in psychoanalysis); the diagonal case occurs in anthropology, where anthropologists inquire into the cultural conditions of their own research (and of course, the Levi-Strauss of Tristes Tropiques and La Pensée Sauvage comes to mind); the diagonal case occurs in literature in a great variety of forms and wherever authors refer to their own texts (numerous instances of this occur in the poems of George Quasha in this issue); in physics, where experimentalists must give a physical account of their experimental apparatus; and in contemplative exercises, where an instruction to attend to phenomena in a certain way must be applied to the phenomena of obeying that very instruction.

It is generally not observed that the consequences and relevance of each of these cases depend totally upon the concrete circumstances under which they arise. Yet, most frequently, the diagonal case forces a re-examination of the terms of the particular system, often causing doubt, dismay, or grandiose mystification as the case may be. Wittgenstein believed that many paradoxes and puzzles for thought, being bewitchments foisted upon us by this general exigency of our notational systems, could be banished simply by noticing and disallowing diagonal situations from our languages. This observation led him to dismiss the significance of both the Russell Paradox, which could be handled by simply eliminating self-referential sets from set theory, and the Godel incompleteness theorems, which appeared to him to involve “a puffed up” notion of proof.2

It is well-known that historically there have been three typical responses to diagonal situations: rejection of the diagonal case as meaningless; rejection of the system as incoherent; or expansion of the system into a new dimension. In the first instance, one rejects the diagonal case as meaningless according to definition: psychology disqualifies itself from studying the psychology of its own theorizing, a judge disqualifies himself from sitting in trials wherein he may be a party, transfinite numbers are simply denied existence within the mathematical cosmos. But the problem with such a blanket solution is that, though in some cases self-elimination may be appropriate (the case of the judge for instance), in others, the refusal to confront the diagonal case simply begs the question. It may be quite important to know how the psychology of a psychologist affects his psychological theory, or how the physics of a physicist’s apparatus influences his experiments. Even transfinite numbers, given appropriate constructions, have their uses.

But if the diagonal case is naively accepted, contradictions in the system arise and the system loses its epistemological coherence altogether: some solution to the Russell Paradox must be accomplished, or else the resulting inconsistencies in set theory render the latter useless for founding arithmetic; if the psychological condition of the psychological theorist determines the content of his theory, the theory is deprived of convincingness; and, if the meditator applies the instruction “refrain from intentional activities” to the activity of meditating itself, he will abandon his session.

Where diagonalization is not abandoned, often a new dimension of the discipline in question comes into view. Diagonalization thus seems to be a moment of creative fertility, wherein the limitations of a notational system are reached and new vistas of conceptualization may be opened. But here the dangers are that of grandiosity and mystification, where irrelevant “acts of faith” may be involved. If diagonalization is permitted without restriction, as, for instance, in classical mathematics, we may find ourselves committed to an overpopulated cosmos of abstract entities, actually created by the excesses of the notational system.

The later Wittgenstein’s relentless assault on Platonic idealism has its roots in his objection to diagonalization procedures, for the belief in the existence of platonic forms has its source in the diagonal situation that arises whenever one inquires about the existence not of the entities that fall under a given concept, but of the concept itself.

Particularly poignant and anxiety-provoking cases of diagonal substitution occur for the Buddhist meditator, and I will try to show how the example of the Zen student confronting his Koan is analogous to the style of treating diagonal arguments recommended by the ultra-institutionalist program.

Numerous exercises require Zen practitioners to refrain from conceptual thought, to refrain from activity, or to perceive all phenomena and all thought as “empty” or void. But the thought by which the meditation itself is set in motion is itself a concept, and mediation is itself a kind of activity. Mediators must thus wrestle with the diagonal case propounded by the instruction they are attempting to follow, until a break-through, wherein the experience allowing them to differentiate the appropriate levels of application of the instruction, occurs. Diagonalization, in this way, is at the heart of many Zen “Koans” or “Model Subjects” (as they are termed in the Hekigan Roku, quoted by Hennix below.) The meditator is forced to address a vivid contradiction which has the structure of a diagonal argument.

Now, Zen meditators notoriously face the irascibility of Zen masters, and Zen masters may refuse the student’s solution to the koan for two contrasting reasons: either the student fails to experience the bite of the koan—refuses, that is, to take the contradiction seriously, never actually confronting the diagonal case (such a student is like the formalist theorist who saves the system by rejecting the diagonal case as simply undefined within it—the specific contradiction is resolved, but that is all that has been gained); or else, the student allows himself to grow dizzy with the koan: he experiences a kind of psychic vertigo or ecstasy, allowing the diagonal dilemma to generate hallucinations and grandiose (even transfinite) constructions. His answers to the koan are up in the clouds; his state of mind is inflated and out of touch with the task of confronting the nature of his own mind—the task that is at the heart of the meditative process. The Zen master cuts him down with some direct reminder of his immediate and earthbound condition. Such a meditator resembles the classical theorist, carried away by the Platonistic possibilities of his diagonal constructions.

But successful Zen students are able to see the diagonal construction for what it is and pass beyond it. They attain a vantage point that is not confined or defined by the language in which the meditational instruction is couched. They discover in their own experience the very mind that is struggling with the koan, and they do so not by blanking out all cognitive activity or refusing to confront the contradiction, but by exercising their faculties to the limit. They cover the entire space of their cognitive language and step beyond it—not into an ever more elaborate and mystifying hyper-reality of thought construction, but onto the immediate ground of their own activity. They are thereby able to grasp the condition and the structure of the exercise which brought them to their insight.

The acceptable solution to the koan is eminently practical, but by no means reductive: the concrete, down-to-earth mind of the meditator is by no means the mundane confusion of the unenlightened: it is ordinary mind brought into contact with its experiential basis, capable of saturating, at a single stroke, the space of its own activity. 

The analogy with the ultra-intuitionist position is this: in dealing with the problem of diagonalization, the ultra-intuitionist steers a middle way between reductive formalism and classical ideational realism. Approaches to diagonalization, like approaches to the construction of number systems in general, are multiple, and tailored to meet specific applications. Because the steps in the procedures of construction must be monitored and ordered, and proofs for the actual completion of the steps must accompany their being carried out, the exact range of application of the propositions of the system can be monitored, specified, and varied according to aim and need. It is unnecessary to banish diagonalization altogether, and it is unnecessary to grant unlimited license to diagonal constructions. Rather, the actual procedure of construction is always kept firmly in view, without arbitrarily and obtusely restricting any constructions which might prove to be of use.

• 1Originally published in the same issue of Io, The Yellow Book is a long composite text by Catherine Christer Hennix that has since been re-published in volume two of Hennix’s Poësy Matters and Other Matters (Blank Forms Editions, 2019).
• 2Wittgenstein, Remarks on the Foundations of Mathematics, 2nd ed (Cambridge: MIT Press, 1983), 132.

Catherine Christer Hennix’s The Yellow Book is a work in progress (Part I of which appeared in WCH WAY # 5, edited by Don Byrd and Jed Rasula), and is composed in such a way that between any two pages a new page may be inserted (dense order pagination). It is my ambition to provide a commentary for this text (and its dense ordering) at some point in the future, but here I will confine myself to a general description of the work and a somewhat random discus- sion of some of its salient features.

The Yellow Book consists of excerpts from material written over the last fifteen years, some of which appeared previously as part of Hennix’s Brouwer’s Lattice, Notes on Toposes and Adjoints (both 1976), and 17 Points on Intensional Logics (1979). Notes on Toposes and Adjoints itself was composed from numerous notebooks to accompany an installation of the (E-) environment, TOPOSES AND ADJOINTS, at Moderna Museet, Stockholm, 4 IX-17 X, 1976. The text was published as an adjunction to Brouwer’s Lattice and was at once a catalog for the installation, a specification of its intellectual parameters, and an element in the installation itself. The installation was a work of “Concept Art” more or less as understood and defined by Henry Flynt.

Hennix is presently working towards a re-installation of her environment, which an extended version of the present text will accompany. A description of the non-textual aspects of the installation will enhance our understanding of the present text.

The environment TOPOSES AND ADJOINTS (referred to as in the text) consisted of a body of works (1–3) in different media elaborating intertransmutable and even parallel aesthetic and epistemological processes.

1  A TEXT, exhibited on a wall outside the exhibition room of the environment and sold as the catalog.

2  The installation itself, consisting of a museum room containing acrylic diagrams, monochromatic computer graphics displays, a pair of ultra-black paintings; the diagrams are large-scale wall paintings of presentations of figures implicitly given by the text, the ultra-black paintings painted by the author and executed with pine-soot as pigment for creating an ultra-black color and applied on highly polished (mirror-like) aluminum square-surfaces, the monochromatic computer graphics ultimately reducible to finite texts defining image-specific computer programs.

3  A continuous, composite sound waveform electronically composed in 1970 and left ongoing from that time to the present.

To participate in TOPOSES AND ADJOINTS actually required spending many hours, not to say days, in attendance at the installation. In attending this programmed environment, one might devote oneself to contemplating the composite sound wave form and its formal relationship with the many ways of reading the graphic material as well as the spatial presentation itself while epistemologically guided by a study of the TEXT.

As mentioned above, the various media of the work were conceived in parallel and are systematically reflected in each other. Each medium—painting, waveform, space, or mathematical text—proposes a certain process of composition and follows that process to one or more limit conditions, for example: a surface of a light-metal mirror with particles of pine soot as the ultra-black paintings are executed until they become totally saturated. Though discrete (infinitesimal) particles of soot are applied, this application is continued until an impression of continuous density is reached. At this point, in a sense, an entire world of possible images has been traversed, and yet the final effect—that of a continuously covered surface—repeats and returns to the initial condition, a blankness or mirror stage in which there is no differentiation of parts (so-called chaotic topological spaces). Sustained contemplation of the black paintings in conjunction with the TEXT, however, recovers all stages of the process: the individual particles of soot become visible again, when perceived as “dissolved” into the printing ink of the text of the formal theory chosen to capture all theorems about a continuum of densely ordered ultra-black soot particles and for which the paintings act as “models.” That is, the “visibility” of the individual soot-particles becomes a semiotical process accompanying acts of self-illumination.

The Yellow Book contains an interpretation/translation of certain key passages from Wittgenstein’s Tractatus. I therefore wish to present a discussion of Hennix’s concern with “formal philosophy”—a concern which may seem incongruous in what we might call the post-Wittgensteinian age. 

It is well-known that Wittgenstein, beginning with his return to philosophy in 1929 (after hearing Brouwer lecture in Vienna), progressively abandoned the formal aspects of the enterprise undertaken in the Tractatus Logico-Philosophicus. This process of abandonment culminated, perhaps, in the powerful passages of Philosophical Investigations wherein Wittgenstein renounces many of the aims of formal philosophy: he renounces the ambition to purge natural language of its ambiguities and metaphysical obscurities; he renounces the hope of establishing, once-and-for-all, the logical structure underpinning language, material reality, and human thought; he renounces the pursuit of the chimerical and fascinating aspects of formal, logical thought-—the appearance of depth that logical enigmas display, the appearance of adamantine, crystalline fixedness that logic promises to depict.

Given what I take to be Hennix’s acceptance of the late Wittgenstein’s renunciations, it is necessary to make clear what motivates Hennix’s use of formal vocabulary and logical apparatus, and what justifies his apparent valorization of the Tractatus. (It may be remarked at the outset that in fact the later Wittgenstein by no means abandoned formal philosophy—see, for instance, Philosophical Grammar.)

In order to approach Hennix’s conception of formal philosophy, it is necessary first to look at several possible post-Wittgensteinian motivations for the development of formal philosophies—motivations which certainly do not underlie Hennix’s concerns.

Accepting Wittgenstein’s reasons for renouncing the project of discovering a unique and universal formal philosophical system, one might still wish to make use of formal thinking as a sort of personal “therapy.” Disciplining one’s language, defining terms and issues, and working out systems of inference might appeal as a reasonable procedure for making one’s way through the morass of intellectual life and the chaos of ordinary language. A private individual might choose to formalize his/her thought without making any claim upon public consensus and having no ambition to compete with other systems for universal truth.

Though not at all precluded (during the Rhinebeck seminars Hennix often talked about the Socratic sense of philosophy as a kind of therapy for curing the confusions of the ordinary mind, and Wittgenstein himself often spoke of the work of philosophy being a kind of therapy aimed at eliminating conceptual maladies), such uses of formal philosophy are betrayed by the rhetorical attitude of Hennix’s texts which seem at any rate to aim at a tone of ontological assurance that would make no sense at all for purely private utterance: Hennix’s pronouncements are punctuated by moments that rise to an almost oratorical state of publicity, yet which at the same time limit their absolute claims by opening large questions about the very existence of the texts in which they are enunciated. Hennix states flatly that “reality” is a result of authority. But ontological authority is confined to conditions of textuality, since “Being” remains only formalizable as a term in a text, while the ontological status of the text itself, being unformalizable, is undetermined or incomplete. “Being” is also identified with “discernings” of boundaries occurring within “spaces” which are expressions of modalities of consciousness and guided/directed with the aid of collections of textual signs. “Thought” is inseparable from acts of attention and attention is directed by acts of thought, represented, say, by the shadows of the objects in the ontology of algebraic geometry, again understood as textual structures. But textual structures are inseparable from human aims and situations, so that most of the ontologies in the environment E documented in The Yellow Book are upon reflection both thoroughly constructivist and intuitionistic in that they are not asserted independently of their conditions of construction and are at every point dependent upon subjective acts of thought. They intentionally fail to guarantee the unique logical cosmos to which the rhetorical gestures in which they are developed suggest they might provide access.

The rhetorical appeals to what may appear to be a “vatic,” oracular, or authoritarian logical universality are never what the texts aim at conceptually. This actually should be obvious since Hennix operates throughout within Yessenin-Volpin’s ethical position which at every point bestows upon the reader maximum freedom to reject even proven propositions: proofs are intelligible only in terms of situations where aims are defined; however, the apparent epistemological anarchy is subjected to the restriction that not all propositions are asserted and not all procedures recommended because they are invariably subject to individual choices and purposes. (Cf. Cage, Fahlström, Johns: The very choice suffices to make them one’s own.) Proofs are not obedient to absolute principles but are defined as “fair means of establishing incontestable propositions convincingly”—convincingness being a matter of the logic of individual acceptation. Correctness is relative to aims. Logic itself is defined as the science of avoiding errors and is demanded only where errors are 1. Definable, and 2. Intolerable.

The requirement that logic specify principles of correctness regarding procedures for attaining aims where error is intolerable makes this format of logic not only useful, but an ultimate court of appeal for technological theories. And, of course, the use of formal theories within specific sciences is in Wittgenstein precisely the appropriate place for them. What is interdicted is the metaphysical extension of theoretical truths beyond the concrete sphere of their application. Something like Yessenin-Volpin’s approach is in practice appealed to in every technological situation where other formal theories fail to accommodate themselves to practical exigencies, and, as developed by Hennix, Yessenin-Volpin may be seen as the true inheritor of Wittgenstein’s late work.

But, again, the refinements and improvements of the logic of technology are not the principal aim of Hennix’s work. (One might notice that Yessenin-Volpin’s “eleutheric” ethics not only specifies the logic for technological projects, but also spells out and attempts to justify a hierarchy of ethical aims that would limit the probability of undesirable side-effects attendant upon the accomplishment of technological aims. Thus, the very theory that shows how technological projects might be facilitated actually establishes severe limitations upon their pursuit. Not all sufficient means are justified by an aim, although, necessarily, all necessary such means are.)

There is one more use that is commonly found for formal theories these days—though I don’t think that the reader is likely to mistake this use for Hennix’s own. Formalizations of psychological, social, aesthetic, and many other situations are frequently attempted where these situations are assumed to be understood intuitively well enough so that “common sense” can provide a criterion guiding the formalization. Such formalizations “explain” nothing that is not already contained in common sense, and, though “harmless” in the sense that they seem to pretend little regarding metaphysical universes beyond the familiar world, they can be quite pernicious in that they tend to reify and render fixed precisely the unquestioned assumptions of the social epoch under which they are undertaken.

What then can be said about Hennix’s use of formal philosophy, given her disengagement from the above motives? To answer this question we pass to our second topic.

At a fundamental level of analysis, Hennix conceives the meaning of a proposition to be one of the main subjects of ethics (since the “reality” of meaning is also a function of authority), and, insofar as uncertainty of the meaning-relation is intolerable, the notion of proof will interfere with the notions of semantics. Thus, for Hennix, the meaning of a proposition is neither the concatenation of the meanings of its terms, the truth or falsity of such concatenations when measured against objective states of affairs, nor again the use to which the proposition is put in ordinary life. The logical meaning of a proposition is a function of the associated propositions which establish it.

This may seem to burden the propositions of everyday life to such an extent that they would for the most part become meaningless. This consequence is accepted by Hennix and points to an important second role that proofs play in Hennix’s thought (beyond grounding propositions) which is, in fact, Hennix’s main motive for doing formal philosophy: to allow the thinking consciousness to grasp the extreme degree to which its own perceptions and cognitions are vitiated with uncertainty. We live in a world saturated with cognitions for which we have no demonstrations, and to the degree that we allow this situation to go unexamined, we live in a world that is meaningless when grasped from a certain ethical viewpoint.

This rather severe picture of the state of our cognitive universe, however, is not asserted as an authoritarian dogma (in the style of the positivism of the ’30s) to be imposed by a logical elite upon an ignorant populace; it is solely presented as an experience which can be turned into an instrument to be developed by those with sufficient experience to find a use for it. Because the concept of proof that Hennix adopts comes under the requirements of Yessenin-Volpin’s “eleutheric” ethics, what counts as an acceptable proof for any proposition depends upon the aims inherent in the concrete situation of which the proposition is a part. A proposition is not true or false independently of its use context—yet, with formalization, this context is specifiable within parameters defined as narrowly as one requires. Thus, if one’s concerns were in fact the trustworthiness of perceptions and cognitions in the everyday world, the proof-theory of meaning would be a particularly powerful tool for displaying the extreme degree of unreliability inherent in our ordinary mundane beliefs: one might thus be moved to examine the bases upon which the most elementary of our sensations, perceptions and assertions are constructed, and thus to find how frequently such constructions are, in fact, vacuous. The collections of meaningful assertions about the world turns out in general to be empty. Yet the world, evacuated by the plethora of meaningless assumptions, cognitions, and assertions which normally cloud and clutter it, does not by any means vanish from view: in fact the empty space—the space vacated by the meaningless propositions—turns out to have a populous interior: an interior surveyable without interference from propositional assertion of any kind. (It is in this context that Hennix has formulated a particularly striking interpretation of Parmenides which to some extent also has been brought forward by S. Austin in the work referred to above, and which will be developed in the supplement to this issue of Io.)

I will conclude these remarks with a look at the specific sense in which the notion of “enlightenment” or “self-illumination” is developed in Hennix’s work. I have, on the authority of the text itself, mentioned analogies with Zen meditation, and The Yellow Book is indeed organized around a series of “Model Subjects,” a term which translates “Koan” and which Hennix borrows from the Shaw translation of The Blue Cliff Record (Hekigan Roku). But the analogy is, to some extent, misleading, in that the disciplines or concatenation of disciplines or forms of mental activity described by Hennix are not dependent upon a reference to Buddhist metaphysics as traditional or textual authority, nor upon participation in Buddhist institutions for authorizations of practice. (The parallels, however, between Hennix’s soteriological epistemology and that of the Indian logician Dharmakirti and the development of his thought within the Madhyamika Prasangika school go beyond those drawn in our introduction. I will certainly take this topic up in some detail in the future.) Though the enlightenment sought suggests Buddhistic forms of illumination, the methods and sociology, as it were, remain western, in the sense that they are conducted on the ground of the individual intellect and by the individual—responsible to his/her own intellectual and ethical life alone.

The substance of enlightenment or self-illumination for Hennix begins with an ascesis that aims at the establishment of the Creative Subject’s independence from “mundane” forms of thought and from the ordinary language which saturates and controls ordinary cognitive life. One attempts with unremitting assiduity to identify the forms of thought which rule one’s cognitivity, (the ultimate such forms are one’s “noemas”), and through the application of analytical techniques one withdraws and reduces the streaming of associative thought to which they give rise.

But for Hennix it is insufficient simply to identify and suppress these noemas: the drift of linguistically saturated and alienated consciousness cannot be neutralized by simply observing the concrete content and activity of the movement of one’s mind, for the general structures which determine this drift will remain operative unless they are pacified by constructions aimed precisely at consuming, replacing, or reducing them. The general structural form of their production must be discerned. Such discernings will provide the preconditions for the reduction down to and ultimately of the noemas. Reduction of the noemas is possible, I repeat, through the comprehension of the general structure of thought and the assiduous application of this comprehension to one’s own cognitive activity. Now the discernment of the general form of thought involves an analysis of the linguistic forms in which thought is ordinarily encountered, and in this way Hennix’s work has its roots in a tradition of poetics beginning perhaps with Hölderlin and extending through Mallarme to Blanchot, Lacan, and Foucault. These writers delineate with great subtlety the problematic of the Cartesian subject with regard to its alienation and annihilation through the evolution of an awareness of language as such: the subject loses itself in its reproduction as the “I-speak” of a beginningless and interminable verbal stream, whose origin is inaccessible but whose existence as an ungraspable totality prefigures the entire of the space of individual linguistic consciousness.

But whereas the latter three of these writers base their linguistic thinking on the tradition of Saussure, Hennix works with concepts found in Montague grammar that are in radical competition with specifically the Chomsky school. It is Montague that is, in any case, important for Hennix’s work—in particular for his theories of abstract grammars and higher-order programming languages (logic programs). Montague worked from the premise that all language can be treated as a species of abstract mathematical structure, with the grammars of concrete languages falling out as special cases of purely formal possibilities constructed a priori from set-theoretical considerations. Hennix “lifts” Montague grammar and locates it within category theory, and thus brings it into contact with fundamental logical structures in an atmosphere where the possibility of freely choosing the basic logical laws underlying the linguistic structures becomes available for individually-determined conceptual use. By working with the “forgetful functors,” “pullbacks,” and the “empty category” in ways consonant with but not intended by the originators of category theory, Hennix prescribes a method for eliminating cognitive commitments at a single stroke. Since the possibilities for this elimination are capable of a priori development, criteria can be envisaged by which the individual can test his/her advancement along the path. The application of such criteria are what make it possible for the individual to travel this path without guidance of tradition or teacher.

The condition of enlightenment aimed at, then, is a condition where the Creative Subject has rigorously liberated him/herself from the drift of ordinary cognitivity. The interest of such a condition actually begins at this point: one wants to imagine how the entire domain of human activity might be re-visioned and the entire domain of technology and culture revitalized under such conditions. Unfortunately, all that has been accomplished thus far is the determination of the “way,” though it should be obvious that this has been a formidable task; nonetheless, it is only the beginning of what appears to be an inexhaustible journey. Though the path of The Yellow Book is thoroughly destructive (as is the initiation of Intuitionism through Brouwer’s “first act”), the consequence of this destruction is to introduce profoundly hopeful perspectives into a cultural and historical milieu for the most part dominated by intellectual triviality, myopia, and fatigue.

. . . The intervention of intuitionism of which the first seems necessarily to lead to destructive and sterilizing consequences, whereas, the second yields ample possibilities for recovery and new developments . . .

FIRST ACT OF INTUITIONISM

Completely separates mathematics from mathematical language, in particular from the phenomena of language which are described by theoretical logic. It recognizes that mathematics is a languageless activity of the mind having its origin in the basic phenomenon of perception of a move of time, which is the falling apart of a life moment into two distinct things, one of which gives way to the other, but is retained by memory. If the two-ity thus born is divested of all quality, there remains the common substratum of all two-ities, the mental creation of the empty two-ity. This empty two-ity and the two unities of which it is composed, constitute the basic mathematical systems. And the basic operation of mathematical construction is the mental creation of the two-ity of two mathematical systems previously acquired, and the consideration of this two-ity as a new mathematical system.

It is introspectively realized how this basic operation, continually displaying unaltered retention by memory, successively generates each natural number, the infinitely proceeding sequence of natural numbers, arbitrary finite sequences and infinitely proceeding sequences of mathematical systems previously acquired, finally a continua extending stock of mathematical systems corresponding to “separable” systems of classical mathematics.

THE SECOND ACT OF INTUITIONISM

which recognizes the possibility of generating new mathematical entities:

firstly in the form of infinitely proceeding sequences p1  . . ., whose terms are chosen more or less freely from mathematical entities previously acquired; in such a way that the freedom of choice existing perhaps for the first element p1 may be subjected to a lasting restriction at some following pv, and again and again to sharper lasting restrictions or even abolition at further subsequent pvs, while all these restriction interventions, as well as the choices of the pv s themselves, at any stage may be made to depend on possible future mathematical experiences of the creating subject;

secondly in the form of mathematical species, i.e., properties supposable for mathematical entities previously acquired, and satisfying the condition that, if they hold for a certain mathematical entity, they also hold for all mathematical entities which have been defined to be equal to it, relations of equality having to be symmetric, reflexive and transitive; mathematical entities previously acquired for which the property holds are called elements of the species.

With regard to this definition of species we have to remark firstly that, during the development of intuitionist mathematics, some species will have to be considered as being re-defined time and again in the same way, secondly that a species can very well be an element of another species, but never an element of itself.

Two mathematical entities are called different if their equality has been proved to be absurd.

Two infinitely proceeding sequences of mathematical entities a1, a2 ......., and b1, b2 ......., are called equal or identical if av = bv for each v and distinct, if a natural number s, can be indicated such that as and bs are different.

From L.E.J. Brouwer, Collected Works I, ed. Arend Heyting, North-Holland Publishing Company, 1975.

Originally man lived in isolation; with the support of nature every individual tried to maintain his equilibrium between sinful temptations. This filled the whole of his life, there was no room for interest in others nor worry about the future; as a result labour did not exist, nor did sorrow, hate, fear, or lust. But man was not content, he began to search for power over others and for certainty about the future. In this way the balance was broken, labour became more and more and more diabolical. In the end everyone wielded power and suffered suppression at the same time. The old instinct of separation and isolation has survived only in the form of pale envy and jealousy.

TURNING INTO THE SELF

Having contemplated the sadness of this world, look into yourself. In you there is a consciousness, a consciousness which continually changes its content. Are you master of these changes? You say no, for you find yourself placed in a world which you have not created for yourself, you are bewildered by its continuous state of flux.

The content of your consciousness, however, is to a great extent determined by your moods and these are within your power. Is the motto “Control your passions” only an empty phrase to you? Sometimes you must have experienced that religious feeling of escape from your passions, from fear and desire, from time and space, from the whole world of perception. Finally, you do know that very meaning phrase, ‘’turn into yourself.” There seems to be a kind of attention at a great distance from the Self; we cannot even get near it by reasoning or by words, but only by “turning into the Self” as it is given to us.

This “turning into oneself” is accompanied by a feeling of effort, it seems as if some inertia has to be surmounted, that your attention is strongly inclined to linger where it is, and that the resistance felt in the move towards the inner Self is much greater than in the move away from it. If, however, you succeed in overcoming all inertia, passions will be silenced, you will feel dead to the old world of perception, to time and space and to all other forms of plurality. Your eyes, no longer blindfolded, will open to a joyful quiescence.

……….

Now you will recognize your Free Will, in so far as it is free to withdraw from the world of causality and then to remain free, only then obtaining a definite Direction which it will follow freely, reversibly. The phenomena succeed each other in time, bound by causality because your coloured view wants this regularity, but right through the walls of causality “miracles” glide and flow continually, visible only to the free, the enlightened.

MAN’S FALL CAUSED BY THE INTELLECT

Without pain the free man sees mankind cast down by fear and desire, by avarice and lust for power, by time and space, aimlessly wandering without wings, incapable of lifting itself in self-reflection chained to the spawn of time and space, the Intellect, which has become fossilized in the form of the human head, the symbol of man’s fall.

……….

This highly esteemed Intellect has enabled and has forced man to go on living in Desire and Fear, rather than—from a salutary sense of bewilderment—take refuge in self-reflection. Intellect has made him forfeit the staggering independence and directness of each of his rambling images by connecting them with each other rather than with the Self. In this way the Intellect made him persevere in a state of apparent security in a “reality” which man in his arrogance had made himself, which he had tied to causality, but in which eventually he must feel totally powerless.

In this life of lust and desire the Intellect renders man the diabolical service of connecting the two images of the imagination as means and end. Once in the grip of desire for one thing he is made by the Intellect to strive after another as a means to obtain the former.

……….

The act aimed at the means always overshoots the mark to some extent; the means has a direction of its own, at an angle, however small, from the ends. It acts not only in the direction of the end, but also in other dimensions. Man’s blinkered view prevents him from recognizing the sometimes very detrimental effects of such action, but worse the end is gradually lost sight of and only the means remains.

In this sad world, where a clear view of all human activity is impossible, a world dominated by Drill and Imitation, the other offspring of Fear and Desire, many recognize as an end what was originally only a means. They seek what we might call an end of second order and in so doing may discover a means again out of line with the corresponding end. If this deceptive jump from ends to means is repeated several times, it may happen that a direction is pursued which not only deviates into other dimensions but even opposes the direction of the original end and therefore counteracts it.

Industry originally supplied its products in order to create the most favorable conditions for human life. But one ignored the fact that in manufacturing these products from the resources of nature one interfered with and disturbed the balance of nature and of human conditions, thereby causing damage greater than the advantages of these products could ever justify.

But worse: manufacturing these industrial goods has become an end in itself, new industries were called into existence merely to supply instruments to facilitate production. Another blow was dealt to the balance of nature. Raw materials were recklessly seized from far away lands, commercial and naval enterprises were created with all their physical and moral misery, all leading to oppression of one people by another.

Now that the Self had been abandoned, the Self that knows all about the past and the future, man grew anxious about the future and craved for power to predict. Science originates in this desire to predict, in its early stages it is completely subservient to industry. Science asserts generalizing propositions in and about the world of perception; these will come true as long as it pleases God, sometimes they are contradicted by the facts. The scientists then exclaim: “Yes indeed , but we had made this or that tacit assumption.” In their incompetence they then set about complicating the proposition further and making so called improvements.

Science does not remain confined to serving industry, again the means becomes an end in itself and science is practised for its own sake. A further aberration has been the concentration of all bodily awareness on the human head thereby excluding and ignoring the rest of the body. At the same time man became convinced of his own existence as an individual and that of a separate and independent world of perception. At this stage the full extent of the deviation of human scientific thinking became clear, for scientific thinking is nothing but fixation of the will within the confines of the human head, a scientific truth no more than an infatuation of desire restricted to the human mind. Every branch of science as it proceeds, will therefore always run into trouble; when it climbs too high it becomes blindfolded in even more restricted isolation, the remembered results of that science take on an independent existence.

The “foundations” of this branch of science are then investigated and this soon becomes a new branch of science. Then one begins to search for the foundations of science in general and knocks up a “theory of knowledge.” As they climb higher and higher trouble increases and in the end everyone is thoroughly confused. Some in the end quietly give up. Having thought for a long time about the elusive link between the intuiting consciousness—which itself develops from the world of phenomena—and this world of phenomena (which again itself exists only through and in the form of the intuiting consciousness)—a confusion which originated in a sinful foundation of the world of intuition, they then plug the whole with the concept of the Ego which was self-created with and at the same time as the phenomenal world. And then they say, “Yes, of course, something must remain incomprehensible and that something is the Ego that comprehends.” But there are others who do not know when to stop, who keep on and on until they fancy that in this way equilibrium is within reach and almost reached. So much for science, the last flower and ossification of culture.

Even if Conscience penetrates into the enclaved categories, man’s attention is diverted away from it by the strongly felt stimulation and satisfaction of other needs, or it is assimilated, i.e. it is recognized as a need within the closed system and capable of satisfaction in the system. The main function of art and poetry but also of religion is to silence the human conscience by recognizing this need and by apparent but not real satisfaction. Art and religion in this world are only morphine industries, the yearning for a better life is only lulled into sleep or into a state of torpidity.

RECONCILIATION

This corrupt world, as you now recognize, only exists because of its very corruption, its deviation from the paths of rectitude. A world of righteousness seems to you as contradictory as your own mortality.

In language transcendent truth—even less than immanent truth—cannot be revealed without causing an outrage. A clear and true statement, seriously and emphatically pronounced, is no more acceptable than the manifest performance of a miracles.

……….

In language transcendent truth seems to be the prerogative of imitators who have vaguely understood the words of the prophet and recognized them as truth, but only after watering it down to suit themselves.

……….

They will liberate the world of all sorts of vices, stupidity and injustice, and be hailed as the benefactors of mankind but leave mankind as miserable as it was.

……….

The advice to get rid of the intellect, “this gift of the devil” is qualified by some added remark in defence of the viewpoint of the repudiated intellect, such as for example: “The structure of nature is so infinitely subtle and complex that your intellect will never fully grasp it and so you will never find there the stability you aim for.” For those who relinquish the intellect, however, the world is anything but subtle or complex: it is immediately clear: it appears subtle only to the intellect that struggles laboriously and sees no end to its struggle.

……….

Look at this world, full of wretched people, who imagine that they have possessions, afraid they might lose them, always hopefully toiling in an effort to acquire more, look at people who strive after luxury and wealth, at those whose riches are secured, whose stocks and shares are safely deposited, but who nurture an insatiable appetite for knowledge, power, health, glory and pleasure.

Only he who recognizes that he has nothing, that he cannot possess anything, that absolute certainty is unattainable, who completely resigns himself and sacrifices all, who does not know anything, does not want anything and does not want to know anything, who abandons and neglects everything, he will receive all; to him the world of freedom opens, the world of painless contemplation and of—nothing.

From L.E.J. Brouwer, Collected Works I, ed. Arend Heyting (North-Holland Publishing Company, 1975).