Domains of Variation

The art and writings of C.C. Hennix draw extensively upon certain kinds of mathematical formalism, most prominently category theory and categorical logic, but also set theory, type theory, L. E. J. Brouwer’s intuitionism, intuitionistic logic, Alexander Esenin-Volpin’s ultrafinitism, and David Hilbert’s proof theory (or her interpretation of it). In particular, her published writings of the 1970s and ’80s, works like The Yellow Book (1989) and Notes on Toposes and Adjoints (1976), contain a vast array of mathematical machinery presented within an even larger kaleidoscope of references, including early analytic philosophy, Eastern thinking, Japanese Noh drama, formal linguistics, and other topics.

While these writings were not intended as systematic, and have an avowedly esoteric and fragmentary quality, it is interesting to consider what attracted Hennix to the mathematical concepts she sought to employ, and how these references relate to her better-known output as a composer and artist. It is a curious and almost characteristic feature of these works that in spite (or perhaps because) of their richly variegated standpoint, they make little effort in the way of explaining themselves. Their poetic, formal, and collage-like character lends them an introspective or inward-looking quality, which both mirrors and obscures the meanings of the texts. This paper aims to give some clarity to those writings, providing an ambient theory that encompasses Hennix’s technical, aphoristic, and often speculative prose.

Although these texts resist any complete interpretation, it is instructive to place them in the context of her substantial artistic engagements, with the music of La Monte Young and Pandit Pran Nath, and her ongoing collaborations with Henry Flynt. One could choose to adopt a technical viewpoint and evaluate specific claims in the texts. In the end, however, it is more fruitful to paint a somewhat broader portrait, one of a highly original artistic and intellectual milieu arising out of an unlikely confluence of mathematics and the 1960s avant-garde. While there are several ways of approaching this task, I will focus first on Hennix’s interest in category theory as it relates to her engagement with the music of Young, and second on the act of semantical interpretation as it pertains to her ongoing dialogue with Flynt.

As is clear from the first paragraph, Hennix’s primary mathematical interests lie in logic, and more specifically nonstandard foundational positions for mathematics. While the viewpoints she drew upon seldom became widely adopted (and in some cases are almost completely unknown within the mathematics community), in a more general sense they do intersect with important (and non–philosophically motivated) developments in twentieth-century mathematics. Any substantive foundational theory should arise out of mathematical practice, and indeed set theory, category theory, and type theory developed out of significant problems in analysis, topology, and the theory of computation. Furthermore, as we shall discuss later, the notion of a topos, a central concept in her work and one to which she ascribes a great deal of philosophical importance, initially arose as a tool for tackling important problems in topology and algebraic geometry.

When convenient, I will adopt a more general mathematical viewpoint for ease of exposition, even if this standpoint isn’t explicitly advocated in the writings. Indeed, while her use of a topos often hews closely to the logical conception of a “universe of sets,” the topological perspective may in fact be more relevant to her underlying interests.

To begin, I will provide some general mathematical background necessary to make headway into the writings. One could go a ways in this direction, but I will restrict discussion to the most pertinent concepts: a description of the classical continuum, Brouwer’s notion of a choice sequence, and some background in the development of category theory.

One initial point of confusion (and sometimes terminal boundary) surrounding Hennix’s work is that she uses mathematical terminology for nonmathematical purposes or assigns it extra-mathematical meanings. For instance, besides being a category satisfying certain axioms, in these writings a topos often refers to a “modality of thought” or “state of consciousness.”

In fact, much of the mathematical formalism Hennix adopts is at some point or other reinterpreted in a not-fully-defined language of introspection. For instance, she often views Brouwer’s Creative Subject as an uninterrupted stream of sensations to which “mental operations” may be applied. In Excerpts from Parmenides and Intensional Logics, she suggests that “the minds mental operations are: ATTENTIONS (arrows, sets), COLLATIONS (=, ≠), CONNECTIONS (CON, θ_ω), MEMORY/RECOLLECTIONS (?_ω), PERCEPTIONS (∧_ω), and INTENSIONS (∨_ω)” before resuming a poetic dialogue surrounding “Mind, upon entering the domains of the Metaxyan Galaxy, in communion with Kosmos.” 1  In many cases, philosophically suggestive or poetic couplings are made between widely different arenas, but these leaps are indicated within the mathematical formalism at hand. As any connection between these pairings cannot be expressed in the language in question, some confusion arises as to the intent of using formal languages, adding to the esoteric quality of the texts. While the precision of mathematical language has a poetic appeal, yielding connotations that might not appear in more expository contexts, it seems that the arguments, given their emphatic nature, would be better expressed in a natural language setting. Indeed, Myles Tierney (one of the founders of topos theory) supposedly remarked that Hennix had succeeded in reintroducing all the vagaries in the subject that he and F.W. Lawvere had spent their professional lives trying to remove.

On the other hand, it is not difficult to locate Hennix’s approach in certain mathematical precedents. For instance, the notion that mathematics can be used to formalize a mode of thinking has several highly interesting precursors. One aspect of Brouwer’s intuitionistic program was a mathematical description of a process of introspection (although it should be emphasized that Brouwer developed a complete and rigorous mathematical theory). Similarly, at various points Hilbert claimed his proof theory was “nothing else but a formalization of our process of thought.” Going further in this direction, in What Are Numbers and What Should They Be? Richard Dedekind “proves” the existence of infinite systems by devising a bijection between a collection of thoughts and one of their proper subsets. In this case, the existence of an infinite system is justified by an appeal to a process of introspection. It is in this context that one can locate Hennix’s attempts to wed mathematical formalism and internal or introspective states.

Furthermore, one can trace her specific interest in topos theory to her time spent at the University of California, Berkeley, as an exchange student. In 1971, the twenty-three-year-old Hennix arrived at one of the leading centers of logic research in the world, Berkeley’s Group in Logic and the Methodology of Science. By this time, she had already composed several electroacoustic compositions at Elektronmusikstudion Stockholm (EMS), one of the world’s leading centers for electronic music, which had been anthologized and performed at major museums. She had met and begun work with La Monte Young (and in 1970 realized one of his Drift Studies using the new phase-locked oscillators at EMS), and was an active jazz drummer who would soon appear with Don Cherry on the soundtrack to Alejandro Jodorowsky’s The Holy Mountain (1973). At the same time, she was a student of linguistics, philosophy, and mathematics at Stockholm University. While at Berkeley, besides working on logic, she began her extensive raga studies with Pandit Pran Nath, who was teaching at Mills College in Oakland at the invitation of Terry Riley. Let us now set the scene of Bay Area mathematical logic at the time of Hennix’s arrival.

In 1963, the Stanford mathematician Paul Cohen introduced his method of forcing, a revolutionary technique for constructing new models of set theory. He amazed the mathematical world by using this method to prove the independence of the continuum hypothesis from the standard axioms of set theory (called ZFC), later winning a Fields Medal for this effort. However, a new method can be more valuable than even the most substantial result, and there was a concerted effort within the logic community to understand this new construction.

            By the mid- to late 1960s, Robert Solovay and Dana Scott (who were then teaching at Berkeley and Stanford) reformulated Cohen’s approach in algebraic terms, in the form of “Boolean-valued models” of set theory. Shortly thereafter, two prominent category theorists, Lawvere and Tierney, interpreted these Boolean-valued models in terms of categories of sheaves on Boolean algebras, in effect expressing them in the language of category theory.

In 1966, Lawvere encountered Alexander Grothendieck’s notion of a topos, which generalized the notion of a sheaf on a topological space. Lawvere and Tierney saw foundational significance in this notion and axiomatized the related concept of an elementary topos in 1969–71. Almost immediately, the “Boolean-valued models” of Solovay and Scott (or their categorical expressions) were seen to satisfy the axioms of a topos, which in turn allowed much of Cohen’s original forcing technique (and in particular the construction of new models of set theory) to be translated into the language of category theory. From a logical perspective, a topos could now be viewed as a “universe of sets,” although initially it was conceived as a vastly generalized topological construction.

This was state-of-the-art work in logic when Hennix arrived at Cal. One can detect in this setting a longstanding and pervasive influence on her output. Indeed, Solovay, who was then a young faculty member at Berkeley and had recently completed his PhD under Saunders Mac Lane (one of the founders of category theory) at the University of Chicago, was a key contributor to all of these developments, and his work, along with that of the constructive proof theorist Georg Kreisel at Stanford, seemed to exert a particularly strong influence on Hennix.

Locally, many of the notes on category theory appearing in The Yellow Book and Notes on Toposes and Adjoints were compiled from discussions with students and faculty during her time at Berkeley. Her compositions of this period, pieces including Forcing (1973), Fixed Points (1973), and □_k (1976), are expressed entirely in the language of set theory and deal with Boolean-valued models, large cardinals (infinite sets with size much greater than what is typically required to do mathematics), and other topics she encountered as a student. Furthermore, the construction of the famous Solovay model in 1970, which uses forcing and the existence of a large cardinal to construct a model where the classical continuum has nicer properties than is typical (every subset is Lebesgue-measurable), seems an interesting precursor to Hennix’s later repeated attempts to find new models for a “continuum of [musical] intervals,” as she proposes in Forcing.

One can detect how Hennix, through her formative experiences as a student, arrives at certain central themes in her work. However, this does not necessarily explain the intent of her project or illuminate the connections she was trying to draw. Given the fragmentary, formal, and most commonly poetic nature of the writings, it is not reasonable to expect a systematic answer to this question. Nonetheless, it is instructive to look towards the mathematical concepts Hennix employs. In general terms, they relate to formalizations of continuous phenomena, or intensional theories (based on the senses of terms) rather than extensional ones (which concern the abstract existence of objects).

In many cases, the mathematical formalism she adopts (intuitionism, topos theory, type theory, etc.) is concerned with expressing continuity as a primitive notion, rather than as an additional layer of structure added upon a discrete or extensionally defined collection of objects. This experiential notion of continuity provides a central undercurrent to her writings, and she likely saw mathematical language as an exact tool for delineating this concept. Indeed, it is precisely this synthetic process that Brouwer sought to characterize with his intuitionistic continuum.

Although never explicitly stated in these terms, this is also almost certainly the connection Hennix wished to establish between mathematics and her other artistic activities. In particular, it is exactly this kind of synthetic construction that underlies Young’s conception of “tuning as a function of time,” and several facets of his compositions from the 1960s onwards. Similarly, one feature of Flynt’s early concept art was the development of new formal systems for introspective experiences. For instance, in Concept Art Version of Mathematics System 3/26/61 (now titled Illusions-Ratios) (1961/3), “sentences” of the formal language are taken to be perceived length-to-width ratios of the logical symbol “⊥” (hence the “syntax” of the language is composed of synthetic experiences), and deductions are understood as reorderings of these continuous phenomena. These pieces provide a “logic” of the mind’s presentational powers, which proved influential on Hennix.

However, Flynt’s aims were somewhat different than Hennix’s, and he was inspired by different philosophical source material, in particular Rudolf Carnap’s The Logical Syntax of Language (1934) and Ernest Newman and James Nagel’s Gödel’s Proof (1958). Flynt began as an undergraduate mathematics student at Harvard in the fall of 1957 (in the class ahead of Tony Conrad, Saul Kripke, and Ted Kaczynski). During this time, Flynt sampled course offerings widely, including W. V. Quine’s mathematical logic course (both he and Conrad struggled with the final exam, although a drawing Flynt made during class is now in the collection of MoMA) and real analysis and algebraic geometry courses with John Tate, before eventually withdrawing from school in the spring of 1960.

Through his coursework, Flynt became interested in formalism as a foundational position for mathematics. Roughly put, formalism reduces mathematics to syntactic manipulation, or the mathematical manipulation of strings of symbols. However, this syntax may be interpreted on models, which in turn tells you information about structures you are interested in. Flynt perceived a connection between this combinatorial syntactic approach and things like process art and indeterminacy, in particular in the work of Richard Maxfield and John Cage.

In the summer of 1960, Flynt ventured into (in his own phrasing) “unexplored regions of formalist mathematics” by developing purely syntactic formal systems which, in his mind, precluded any notion of a model or interpretation—and hence “meaning” in a traditional mathematical sense. 2  He saw this project, which he titled concept art, as related to mathematical formalism but without the imputed metamathematical significance. Indeed, by binding syntax to perceptual experience (in particular to non-stable perceptual states), Flynt believed he had found a critique of formalism, which he associated with a criticism of mathematics more broadly.

Flynt’s “meaningless” logical systems in turn led him to more general conceptions of “veramusement” and “brend,” which, in logical terms, concern a free play of the mind’s presentational powers. While Flynt had a specific logical paradigm in mind, he also considered his approach from the perspective of new music, in particular the work of Cage. Cage’s attitude toward composition concentrated the “work” in the mental states of the viewer. This proved a significant influence on Flynt’s concept art, and later Hennix’s epistemic art. Indeed, Flynt claimed concept art was an attempt to “apply new music to metamathematics.” 3  Although Cage’s focus on a free play of the mind’s presentational powers was conceived in compositional terms, one might also locate it in classical aesthetics; his notion of “purposiveness without a purpose” is derived (likely via John Dewey) from Kant’s theory of aesthetic judgment. We will discuss this connection at greater length later on.

Through Young, Hennix became aware of Flynt’s work, and they have been close collaborators since the mid-1970s. In many instances, one can sense Hennix adopting a semantical viewpoint on Flynt’s efforts. In his construction of logics of subjective experiences, Flynt follows Carnap’s dictum: “In logic, there are no morals. Everyone is at liberty to build up his own logic, i.e., his own form of language, as he wishes.” 4 Flynt introduces syntactically complex languages (indeed, it is often impossible to precisely specify what the syntax is, given its correlation with a continuum of experiences), where the “logical terms” (being a free play of cognitive powers) preclude any external interpretation.

However, instead of an uninterpreted “logic” of introspective experiences, from a semantical standpoint one could also propose introspective “interpretations” or “non-standard models” of mathematical formalizations, as Hennix frequently does in The Yellow Book—for instance, in her association of toposes with different “modalities of thought.” In this way, while Flynt’s concept art could be considered “syntax rich, semantics poor,” in “Brouwer’s Lattice,” Hennix proposes her work as being “syntax poor, semantics rich,” adding, “Let the Diagrams Commute,” appropriating then-popular slogans from category theory.” 5  Let us now consider some additional mathematical background necessary to evaluate these efforts.

In a classical framework, there is an underlying assumption that mathematics concerns constant structures, even in its attempts to model motion in space or movement in time. Hence set theory, with its primitive notions of elements and membership, became the presumptive foundational position for mathematics, and Richard Dedekind’s “arithmetization of geometry” provides the standard mathematical account of the continuum. From this perspective, mathematics begins with bare sets to which structure, often of a “spatial” variety, is added. One consequence of this analytic viewpoint is that, at a foundational level, the world is viewed principally in discrete or disconnected terms.

The classical continuum provides a striking example of this vantage point. A line is perhaps the most immediately given and intuitable spatial entity, and serves as a common model for both time and space. In standard mathematical practice, the continuum is composed of discrete elements that, taken together, form a single continuous whole. Of course, the way in which these atomistic pieces might fit together to form a continuous whole is one of the most vexing problems in the history of philosophy and mathematics. As Leibniz notes, “There are two labyrinths of the human mind, one concerning the composition of the continuum, and the other concerning the nature of free will, and they both arise from the same source, infinity.” 6

For future comparison, let us briefly suggest a standard mathematical construction of the continuum. The set of natural numbers ℕ = {0, 1, 2, ...} and the set of integers ℤ = {..., -2, -1, 0, 1, 2, ...} can be successively enumerated, and come equipped with a natural ordering “ < .” From the integers, one can construct the set of all fractions by considering ratios of integers up to fractional equivalence (i.e., 1/2= 2/4= 4/8= ...). Together with the natural ordering on the set of all fractions, this yields the rational numbers (ℚ, <). The rational numbers are dense (in between any two fractions there exists another fraction) but “gappy” in the sense that one can define sequences of fractions that converge to no rational number (such as a sequence of fractions that get closer and closer but never reach √2). These gaps appear naturally and frequently. For instance, some gaps arise as solutions to simple algebraic equations like x² = 2. All such gaps are called irrational numbers.

The classical continuum is constructed as a “completion” of the rational numbers, by filling in all missing gaps (such as √2, π, e, etc.). Together with an ordering, this yields the real numbers (ℝ, <), which serve as the standard model of the continuum. Note in this procedure, a line is associated with “real numbers,” which can be expressed in terms of sequences fractions (and thereby reduced to integers and ultimately natural numbers). Hence this process is often referred to as an “arithmetization of geometry.”

One curious feature of this completion is that there are many, many more missing irrational numbers than there are fractions. In fact, while there is a natural way to enumerate all fractions, there is no listing of the missing irrational numbers, even in theory. While intuitively it seems that a few gaps are being filled, in reality the probability of picking a random point on the classical continuum and it being a fraction is zero.

Hence, although each classical real number exists as an independent entity, each with its own place and determined with infinite precision on a line, nearly all of these objects are ineffable in the sense that, taken together, they vastly outnumber the language used to describe them. As a result, this “completion” must necessarily occur in some indirect fashion. At best, almost all of the uncountable infinity of missing irrational numbers can be described as infinite non-repeating decimal expansions, and approximated through finite initial segments of this expansion.

However, knowing an expansion up to any finite stage does not tell us what will happen in the future, and reducing a real number to a breadthless point requires infinite precision with respect to its placement on the line. In this respect, the missing irrational numbers may be viewed as “actually infinite objects”; they can be identified with equivalence classes of infinite sequences of fractions approaching but never reaching the missing gap. But it necessarily takes a full infinite sequence (or function describing this sequence) to completely specify an irrational number. The completion of the continuum can be seen as an abstract process of identifying “points” with these “infinite objects.” Furthermore, this construction can never be fully explicit in the sense that there are too many missing points to describe.

In general terms, topology studies space up to continuous deformation. While one is typically interested in properties of a particular space, in practice it is often beneficial to consider continuous mappings in and out of a space in determining properties of the space itself. This was one of the basic perspectival shifts in mathematics of the twentieth century, as Jean-Claude Pont (via Colin McLarty) notes on the Cantor-Dedekind correspondence: “One can trace the origin of modern topology to the discovery that mappings which transform one manifold into another teach us as much about the manifolds as do the manifolds themselves.” 7  Hence, while abstractly topology studies the coherence of space, at a more practicable level it examines properties preserved by continuous functions between spaces. Indeed, topological objects themselves are frequently identified with such mappings. For instance, a knot is often viewed as a continuous function from a unit circle into three-dimensional space.

It is worth noting that unlike the set-theoretic approach of characterizing objects as sets satisfying certain properties, from a topological viewpoint the ambient space of an object is in some sense “built in” to the object itself. A function from a circle of radius one to 3-space is different than a function from the unit circle to a sphere, just as a knot in three-dimensional space is somehow different than a knot appearing on a sphere. This emphasis on maps between spaces over the spaces themselves is often taken as a starting point for the development of category theory. 8

However, even after adopting the “functional” viewpoint of modern topology, set-theoretic assumptions still underlie the standard formulation of continuity. A topological space is specified by taking a set X and assigning certain subsets of X as open sets (which intuitively correspond to continua, or unions of such regions). Typically, some collection of basic open sets are given, from which all others can be formed. For topological spaces X and Y, continuous functions between X and Y are then defined in terms of preserving properties of open sets (the inverse image of an open set is open). Hence a discrete collection is given first, to which a spatial structure (in this case a topology) is added on top as an additional layer. As noted earlier, this “spatialization” of discrete objects is ubiquitous in mathematical practice: a group becomes an algebraic or topological group by adding a topological structure compatible with the group operation, a collection of abelian groups is parameterized to form a sheaf, and so on.

For the classical continuum, one common basis of open sets is all intervals of the form (q, r) where q and r are fractions (in other words, the set of all real numbers between q and r without including the endpoints q and r themselves). The complement of an open set, i.e., the set of all points not contained in the open set, is called a closed set. For instance, in the classical continuum, any singleton set {s} is closed, intervals of the form [q, r] that contain the endpoints points q and r are closed, etc. To turn an open set (and indeed any set) into a closed set, one adds all missing “boundary” or “limit” points by taking a closure, for instance by adding the endpoints q and r to (q, r). From this perspective, the classical continuum is the completion or topological closure of the rational numbers, as every irrational number is the limit point of a sequence of rational numbers.

Finally, taking appropriate unions, intersections, and complements of all basic open sets gives a σ-algebra. In the case of the classical continuum, this yields the Borel sets, which can be viewed as the “describable” subsets of the continuum. Although a line appears placid and unassuming, general subsets of the classical continuum are known to have quite pathological properties, and indeed are hard to discuss at all. The Borel sets are relatively well behaved and allow one to define intuitive notions like length and size. For general topological spaces, the algebra of open sets will play an important role later on.

L. E. J. Brouwer was one of the most distinguished topologists and mathematicians of the first half of the twentieth century. Perhaps given his topological inclinations, he was dissatisfied with a reduction of the world to discrete terms. Starting as early as his dissertation of 1907, Brouwer suggested the continuum was mischaracterized by a reduction to completed atomistic points. Although he is now best known for his fundamental fixed-point and dimensionality theorems (two of the most important results of early-twentieth-century mathematics), the composition of the continuum was perhaps the most recurrent theme in his work, and a topic he continually revisited throughout his life. He writes: “The continuum as a whole is intuitively given to us; a construction of the continuum, an act which would create all its parts as individualized by mathematical intuition is unthinkable and impossible. The mathematical intuition is not capable of creating other than countable quantities in an individualized way . . . the natural numbers and the continuum are two aspects of a single intuition (the primeval intuition).” 9  Here Brouwer objects to the size of the continuum required to speak of it as individualized points, noting that any “fixed” and discrete reduction betrays both our mathematical intuition and the faculties of our imagination.

While many prominent mathematicians (such as Émile Borel, Sophus Lie, Hilbert, Hermann Weyl, and others) had expressed doubts about the arithmetization of geometry, Brouwer was the first to propose a new alternative mathematical theory of the continuum, one based on a primitive notion of coherence and “stickiness.” The mathematical framework needed for this new theory is called intuitionism.

While it is often thought that intuitionism restricts the rules available to do math, and hence provides a weaker theory of mathematics (Hilbert compared it to proscribing a boxer the use of his fists), in reality it is incomparable to classical math and in many ways strengthens it, in the sense that nice properties that are false in classical analysis are true in Brouwer’s theory. For instance, it is provable that every full function on the intuitionistic continuum is continuous. Conversely, many theorems of classical mathematics, and indeed his own fixed-point theorem, are false in intuitionistic analysis.

Of course, one should expect and indeed hope that two fundamentally different conceptions of the continuum would lead to different mathematical theories. Furthermore, once the differences in conception are accounted for, corresponding “approximate” versions of many classical theorems that fail on the intuitive continuum can be shown to hold given the appropriate statement (the intermediate value theorem, his fixed-point theorem, etc.).

It should be stressed that Brouwer’s alternative continuum is a rigorous mathematical theory. While philosophers going back to Aristotle (and earlier) speculated on the coherence of the continuum, Brouwer proposed a precise mathematical framework modeling one possible viewpoint on these phenomena. Out of this effort came a highly original conception of the relationship between the discrete and the continuous, a model for the act of doing mathematics, and a mathematical theory of introspection. In total, it was one of the most original conceptual developments of the twentieth century, and one that overlaps with other fundamental artistic achievements in a manner not yet fully appreciated. 10

To understand the uniqueness of Brouwer’s contribution, the passage cited above bears further reflection. Following Kant, Brouwer believed the basic irreducible unit of math was a movement of time. While sensations may come and go without producing any noticeable reaction, mathematics proper begins with an act of attention. As Dirk van Dalen nicely summarizes, sensations pass but “at a certain point the subject may actively interfere as follows: the subject notes, or fixes his attention on a sensation, which is subsequently followed by another sensation. The first sensation is stored in memory at its passing away, being replaced by another sensation. The result is that the subject is aware of both the remembered and the present sensation.” 11 Brouwer refers to this act as a “two-ity,” or “the falling apart of one life-moment to the next.” Of course, for any given “two-ity” there are specific qualities associated with each sensation. Through introspection, one can abstract away from these properties. Brouwer writes, “Mathematics is a languageless activity of the mind having its origin in the basic phenomenon of a move of time . . . which is the falling apart of a life moment into two distinct things. . . . If the two-ity thus born is divested of all quality, there remains the common substratum of all two-ities, the mental creation of the empty two-ity. This empty two-ity and the two unities of which it is composed, constitute the basic mathematical systems.” 12  From this fundamental act of introspection, the awareness of time passing, one may construct the natural numbers (first as a two-ity, then a three-ity, a four-ity, and so on), and from this the integers, the rationals, infinitely proceeding mathematical systems, and infinitely proceeding sequences of mathematical systems previously acquired.

There is a subtle but crucial distinction between these systems and their classical counterparts. Rather than existing as completed sets, these constructions occur in time, yielding potentially infinite or infinitely proceeding structures. Hence in the set of natural numbers ℕ = {0, 1, 2, ...} the symbols “...” have a somewhat different meaning than they do in their classical counterpart, in the sense that ℕ does not refer to a completed mathematical object but rather a process of generation. All relevant constructions are both time and subject dependent, and potentially infinite structures are dynamic.

Although it is not immediately obvious, Brouwer’s conception of a two-ity also leads to an interesting resolution to the discrepancy between the discrete and the continuous. He writes, “Ur-intuition of two-ness (two-ity): The intuitions of the continuous and the discrete join here, as the second is thought not by itself, but under preservation of the recollection of the first. The first and the second are thus kept together and the intuition of the continuous consists in this keeping together (continere = keeping together). This mathematical ur-intuition is nothing but the contentless abstraction of the sensation of time. That is to say, the sensation of ‘fixed’ and ‘floating’ together or of remaining or changing together.” 13  In other words, between every distinct two-ity, there is an entire continuum of events, namely the continuous movement of one moment of time to the next. Hence numbers and the continuum are given to us simultaneously and inseparably, one as the observation of time passing and the other as what happens between these two moments. This is the meaning behind Brouwer’s comment that “the natural numbers and the continuum are two aspects of a single intuition.”

What happens between two acts of attention cannot be reduced to a collection of atomized points. It is not “exhaustible by the interposition of new units and therefore can never be thought of as a mere collection of units.” 14 Instead, this continuum is constituted through choice sequences: never-finished creations developing in time according to an idealized mathematician’s attention. Some choice sequences (the lawlike ones) are completely determined and can be thought of as explicit algorithms, while others (lawless sequences) are generated quite freely by the subject. (It is a subtle distinction, but while in descriptive set theory real numbers are often associated with completed infinite branches of a tree called a Baire space, choice sequences may be viewed as the finite branches of this tree as they develop in time.)

Irrational numbers were previously seen as “actually infinite” or (with some abuse of notation) “transcendental” objects, in the sense that they were identified with infinite sequences of fractions approaching them, or placed with infinite precision on a line. Choice sequences, on the other hand, are always potentially infinite, and contain a slight halo of “blurriness” in the form of a tail that is never fully resolved. It is never precisely clear where they are, and there is always a small (but clearly defined) amount of wiggle room for where they will head in the future. Hence in this setting a real number is divested of its abstract discreteness. Instead, in Brouwer’s conception, one sequentially chooses nested closed intervals of the form λ_n = [ ^a⁄2ⁿ, ^a+2⁄2ⁿ], a ∈ ℤ, n ∈ ℕ. In particular, the continuum as a whole is not a fixed creation to which dynamic properties are added as an additional layer of structure; it is in its fundamental nature dynamic.

Mathematically, the discrepancy between the intuitive and classical continuum is expressed in terms of Brouwer’s weak-continuity principle, which asserts that well-defined properties of choice sequences are determined at some finite stage of development. 15  From this principle, it can be shown that no natural ordering “ < ” exists on the intuitive continuum, as it does for the classical continuum (ℝ, <). For instance, it is provable that there exist choice sequences x such that “x < 0 or x = 0 or x > 0” is false. This, of course, matches the informal description of blurriness given in the preceding paragraph.

The continuity principle concisely expresses the strong coherence and connectedness of the intuitive continuum. As van Dalen notes, “The continuum of Brouwer shows a strong ‘syrup-like’ behaviour; one cannot cut up the continuum into two parts, because in the act of cutting the status of a large number of reals is left open, e.g. suppose one wants to cut the continuum at the origin, then there are lots of points for which a > 0 or a < 0 or a = 0 is unknown.” 16  Brouwer explicitly produced such “underdetermined real numbers” as so-called “weak counterexamples.” Unlike its classical counterpart, the Brouwerian continuum cannot be reduced to any underlying static framework or constant structure. It expresses the primordial coherence of the intuitively given continuum, formulated in a rigorous mathematical setting.

By the 1940s, many deep theorems in topology (such as Brouwer’s fixed-point theorem) had been reformulated in algebraic terms, specifically in the language of homology and its close relative, cohomology. Several homological theories existed by then, each with their own distinctive character and results. These methods associated algebraic structures such as groups to topological spaces, in effect producing “algebraic images” of topological spaces.

In general, topological spaces are unstructured and difficult to distinguish. For instance, it is not easy to imagine whether two four-dimensional spaces in a six-dimensional space can be continuously deformed to each other. By contrast, algebraic objects are quite rigid. Associating these rigid “invariants” to topological spaces proved the most fruitful method for distinguishing topological spaces and approaching the problem of classifying particular families of topological spaces.

Category theory was initially developed as a tool for abstracting the commonalities between these different homology theories and providing a unified framework for performing homological calculations. There are many different kinds of categories: categories of sets, categories of groups, categories of vector spaces, categories of topological spaces, and so on. The basic components of each such category are objects and morphisms. Intuitively, objects are the structures in question and morphisms are the appropriate mappings between these structures. For instance, in the category Set, the objects are sets and the morphisms are functions between sets; in the category Top, the objects are topological spaces and the morphisms are continuous functions between topological spaces.

Crucially, it is possible to define maps between categories (functors) and maps between functors (natural transformations). Using these tools, it is possible to transfer properties from one category to another, and hence results and constructions from one area of mathematics to another. As Allen Hatcher poetically notes, functors provide the “lanterns of algebraic topology” projecting algebraic images of topological spaces. 17

Although not originally conceived in foundational terms, category theory abstracts many of the fundamental patterns and constructions appearing in mathematics. Furthermore, certain constructions that are intuitively clear in familiar categories like Set—for instance products, disjoint unions, and forming the collection of functions between two sets—can be generalized and shown to exist (or not) in other categories. As certain general mathematical constructions can be carried out in any category possessing an appropriate list of properties, one can organize vast mathematical conceptions from a simple axiomatic standpoint, providing something of an atlas of the world of mathematical constructions.

It was quickly observed that many logical concepts could be expressed in categorical terms. In the present context, the most important one is the notion of a model. In logic, a model provides an interpretation of some collection of syntactic statements, a structure on which all of the statements hold. For instance, one might have a collection of algebraic equations—say, the axioms of a group. The collection of all statements that follow from these axioms would be an “algebraic theory,” namely the “theory of groups” (often written Th(G)). Note Th(G) is a purely syntactic collection, but at the same time provides all statements derivable from the axioms of group theory. Of course, these statements will all hold on any specific group of interest. Intuitively, a model picks out a specific group satisfying all the statements. It assigns to the variables in each equation elements of the group under consideration.

In his 1963 thesis, Functorial Semantics of Algebraic Theories, F.W. Lawvere saw that these “algebraic theories” could be axiomatized categorically, in terms of categories having “finite products.” Given this context, he showed that a model of an algebraic theory was a functor from a category with finite products to the category Set (which preserves finite products). Hence a model can be viewed as an arrow or map between categories; a model provides the “meaning” or “interpretation” of a collection of syntactic statements.

This notion that arrows represent meaning is a recurrent theme in Hennix’s work. For instance, adopting a Wittgensteinian tone, she notes that “the world consists of arrows . . . each arrow is a fact—a mental fact.” 18  As we shall discuss momentarily, she derives her notion of “algebraic aesthetics” from the algebraic semantics of Lawvere.

In classical mathematics, we have seen set-theoretic constructs used to form constant structures, to which “spatial” properties are added as an additional layer of structure. In this classical framework, continuous variation of space is modeled through the notion of a sheaf. A sheaf can be viewed as rule F, which assigns to each point x in a topological space X a set F_x consisting of the “germs” at x, typically taken as the functions defined in a neighborhood of x. The sets F_x for all x can then be “pasted” together to form a space projecting onto X. Viewed in this light, the sheaf F is a set F_x, which “varies” (with the point x) over the space X. 19  The base space X is called the domain of variation.

The collection of sheaves on a given topological space X form a category Shv(X ). Sheaves are one of the most fundamental topological constructions. In the early 1960s, Alexander Grothendieck developed a generalization of this notion to settings far beyond sheaves of functions on topological spaces. These generalizations were categories called toposes, and he considered them to be “generalized spaces” or “spaces to do mathematics.” Just as cohomology was originally developed to give algebraic invariants of a topological space, Grothendieck showed how cohomology could also be used to find algebraic invariants of a topos. He then used this technique to solve some of the most important problems in twentieth-century mathematics.

As early as 1963, Lawvere began to conceive of category theory as a viable alternative foundational position for mathematics. Instead of sets and membership, the new irreducible concepts could be objects, morphisms, functors, and natural transformations. In fact, since objects could in some sense be identified with identity morphisms, the notion of an arrow could be taken as the underlying primitive concept of mathematics, without reference to further set-theoretic constructs. As Colin McLarty astutely notes, in set theory the only structure preserved by functions is identity, whereas in category theory “arrows reveal structure,” or “arrows are used to define structure.” 20  Of course, this required translating set theory (or set theory and some part of first-order logic) into the language of category theory, and in 1964 Lawvere published his initial attempt, The Elementary Theory of the Category of Sets.

In 1966, Lawvere encountered Grothendieck’s notion of a topos, which he initially conceived as a possible framework for developing a synthetic version of differential geometry. Between 1969 and 1971, Lawvere and Tierney axiomatized the notion of an (elementary) topos as a category with suitable “limits,” “exponential objects,” and “subobject classifiers.” In fact, this axiomatization closely resembles Lawvere’s categorical axiomatization of sets from a few years earlier. Each axiom of a topos also holds as an axiom of set theory. However, a few statements typically taken to hold in classical set theory (for instance the axiom of choice and a “well-pointedness” axiom) are absent from the axioms of a topos. Both of these excluded axioms are incompatible with continuous variation, and in fact fail on many categories of sheaves.

In this way, a topos permits a wider and more general conception of space than the standard set-theoretic perspective. Furthermore, it allows for a range of possible spatial structures for doing mathematics that are continuously variable in an intrinsic sense, and not reducible to discrete terms.

Lawvere envisioned his categorical approach explicitly with such notions in mind, and with avowedly philosophical motivations. He writes:

The (elementary) theory of topoi . . . is a basis for the study of continuously variable structures, as classical set theory is a basis for the study of constant structures. . . . As Engels remarked in the period when set theory and the arithmetization of geometry did not yet dominate mathematical thinking, the introduction of the advance from constant quantities to variable quantities is a mathematical expression of the advance from metaphysics to dialectics, but many mathematicians continued to work in a metaphysical way with methods which had been obtained dialectically (Anti-Duhring, in the section on Quantity and Quality). . . . Every notion of constancy is relative, being derived perceptually or conceptually as a limiting case of variation and the undisputed value of such notions in clarifying variation is always limited by that origin. 21

As we shall see, this notion of constancy as the limiting case of variation provides a significant undercurrent to Hennix’s writings, as well as to La Monte Young’s notion of tuning as a function of time and Flynt’s concept art.

As a final piece of mathematical background, one axiom of a topos bears special consideration: the existence of a “subobject classifier,” often notated Ω. This can be used to describe the subobjects of an object in a category, and in some sense captures the internal logic of a topos. For instance, consider the example of a category of sheaves of sets on a topological space X. For any open set U of X, Ω(U) describes the set of all open subsets of U.

This is an important example. As mentioned earlier, for any topological space X one can form an algebra of open sets of X. It is easy to see that this algebra can be represented in terms of propositional logic. A propositional variable p can be associated to some particular open subset U of X (in other words, in the relevant topological semantics, propositional letters are assigned to open subsets of X). However, ¬p, the complement of p in X, is not in general an open set, and hence may not be in the relevant algebra. Instead, ¬p should refer to the union of all open sets contained in the complement of p in X (the union of any collection of open sets is always open). In particular, this entails that ¬¬p does not imply p: the complement of the complement of an open set need not equal the open set with which one started. This is logically equivalent to saying it is not the case that “p or ¬p” holds. Hence in general the law of excluded middle fails for the internal logic of a topos. It may hold on some toposes, and not hold on others.

Recall this treatment of negation (and the law of excluded middle) also underlies the logic behind Brouwer’s intuitionistic continuum. For instance, there are many real numbers (so-called weak counterexamples) where x < 0 or x ≥ 0 does not hold. In both cases, it is the dynamic nature of the structures in question that precludes certain either-or statements from holding.

In general, the internal logic of a topos is intuitionistic. The relevant algebra is called a Heyting algebra (named after Brouwer’s student who developed intuitionistic logic), or sometimes a Brouwerian lattice. As Lawvere notes:

The internal logic of a topos is always concentrated in a Heyting algebra object. If this object happens to be Boolean [i.e. a Heyting algebra with classical negation], then the variation of the sets is (constant or) random in the sense that for every part b of the domain of variation the topos splits as a full product ? = ?/b × ?/b′ , i.e., any motion over b and any motion over the complementary part can be combined into a total motion admitted by ?, whereas for most topoi there is a continuity condition at the boundary of b; this is of course analogous to the contrast between continuous and measurable variable quantities. 22  

If the subject classifier is a Boolean algebra, it has the typical separability properties of the classical continuum. However, in a more general Heyting algebra that is not Boolean, stronger coherence properties may apply, as occurs in Brouwer’s intuitionistic continuum.

In 1971, Hennix arrived at UC Berkeley as an exchange student. As detailed earlier, she began work on her Infinitary Compositions, which stretch through much of the 1970s. In the summer of 1973, she wrote a proposal to teach a course on this topic at Mills College. The proposal still exists, although the course was never offered.

Her early pieces such as Forcing, Fixed Points, and ◻_? are written in the language of set theory and concern Boolean-valued models, large cardinals, and other topics. As mentioned earlier, Hennix found Solovay’s work on these topics influential. Indeed, parts of Forcing appear to be derived from Section 1.1 of Solovay’s A Model of Set Theory in which Every Set of Reals Is Lebesgue Measurable, or perhaps course notes on this topic. In comparison with her compositions from a few years later, Hennix colors within the lines of set-theoretic formalism in these early pieces, with none of the extra-mathematical interpolations and excursions that characterize her later work. In one sense, these pieces are more restrictive than her later efforts, in which mathematical terminology is blended and given additional treatment layers. For instance, a few years later, she theorized encountering her infinitary composition ◻^N as follows:

At the moment the Creative Subject enters a frame for a topos ? as defined by the interior of E′, the time manifold ◻^N  is supposed to already contain indefinitely many time elements which have not yet or never will be experienced by the Creative Subject. . . . [Later] at “transfinite stages” of experiencing ◻^N the Creative Subject arrives at a stationary subset of the generated continuum of perceptions at which she retains complete faculative control of the continuum of time-elements which defines the transfinite time-object ◻_?, where ? denotes an ordinal of some large cardinal and not merely a large number as connoted by the symbol N. 23  

Although she employs a considerable amount of set-theoretic terminology, Hennix mixes together Brouwer’s intuitionism, topos theory, topology, and acts of introspection. She combines a set-theoretic result concerning the existence of fixed points on any monotone increasing function from ordinals to ordinals, the experience of a “constant event” of a repeating composite waveform, and Brouwer’s Creative Subject to describe a composition involving three sine tones. In essence, the Creative Subject encounters these rationally tuned sine tones, and the “topos” in question can be viewed as a state of consciousness or the acts of attention that the Creative Subject chooses to devote to this composite waveform. The constant event is the experience of the composite waveform repeating in time. We will describe this setup more precisely in a moment.

The sparsity of the composition relates to attaining maximal clarity regarding one’s own acts of cognition. (Hennix often refers to Occam’s razor or “the law of sufficient reason” when weighing the addition of elements or structural components to her compositions.) In this way, the sound waves function like notation or syntax for focusing one’s attention, similar to the perceived length-to-width ratios in Flynt’s Illusions-Ratios. We will discuss the relationship of sine tones to Brouwer’s “empty two-ity” shortly.

Following Brouwer, Hennix believes that spare introspective acts, such as the act of doing mathematics, can lead to mental freedom from what she calls “the Mundane World,” or what Brouwer called “the Sad World.” For instance, Hennix notes that the “topos” under which one attends only to one’s act of attention (i.e., Brouwer’s empty two-ity) is where “the Creative Subject realizes a complete sense of (perceptual or cognitive) freedom.” 24  

While Hennix’s earliest infinitary compositions have a more cohesive quality internally, in the sense that they are located within a pure set-theoretic formalism, viewed externally they are in some ways even more cryptic. They are compositions in an abstract sense, as there is no obvious auditory content. The sole acoustical reference occurs in Fixed Points, where she provides a method of enumerating just intonation musical intervals in passing. The compositions offer little indication of their meaning to someone not enrolled in the topics courses in set theory Hennix attended, and even then shed little insight into how they might function as compositions in a traditional sense.

Like her writings, these compositions divulge little context of the thought process surrounding their creation. They seem to exist purely as internal acts in the mind of the observer, in which the state of mind or attitude generated by the piece (regardless of content) becomes a part of the composition itself. As we will discuss later, there is a certain Cageian aspect to this reasoning. In slightly more general terms, however, these pieces also reflect on the nature of musical intervals and what constitutes a continuum of experiences in terms of different conceptions of mathematics (for instance, in Forcing, she attempts to construct a “continuum of [musical] intervals” as fixed points of an ordinal function). From this perspective, the pieces provide a nascent picture of themes that will develop in her work.

Musical intervals are commonly represented as frequency ratios, and hence may be “arithmetized” in a fashion similar to the classical continuum. An octave has the frequency ratio 2/1 and so can be associated with the real number 2/1= 2; a fifth can be understood as the frequency ratio 3/2 = 1.5, a fourth 4/3 = 1.33 . . . , and so on. Furthermore, some common intervals are classically represented as irrational numbers: for instance, a tritone has the frequency ratio √2/1. Following this reasoning in a suitably abstract fashion, any point on the classical continuum, or on the continuum (1, 2), can be identified with a musical interval to form one model of a “continuum of musical intervals.”

However, individual points on the classical continuum are located with infinite precision on a line, which is not replicable in any acoustical environment. Another difficulty with this correspondence is that there are an uncountable infinity of distinct points on any line segment. Thus uncountably many musical intervals “exist,” yet there is no way to refer to them or to know if they have been performed.

While a familiar mathematical quandary, this question of abstract “existence” as opposed to realizability became a theme central to conceptual works coming out of the sixties avant-garde, in particular the word scores surrounding the publication of An Anthology. For instance, Young’s Composition 1960 #15 reads: “This piece is little whirlpools out in the middle of the ocean.” This is an unusual piece for Young; even the most conceptual of his word pieces are in general performable and moreover realized in a highly constructive manner. However, this specific piece provides an archetypal nonconstructive statement. It asserts the existence of an object without providing a means of locating it.

Flynt’s response to Young’s Composition 1960 #10 (in which a line is printed on a note card) is an even more explicit commentary on this topic. The 1961 “score” contains a line drawn on a sheet of paper together with the statement: Each Point on this Line Is a Composition. Flynt’s piece asserts the “existence” of an uncountable number of compositions (or at least some continuum of compositions), almost all of which in a classical setting are both unrealizable and unidentifiable. Flynt’s 1961 Work Such That No One Knows What’s Going On operates along similar lines, and in fact one could view Each Point as a model of it.

The notion of modeling a continuum of experiences (or a continuum of intervals) is a theme common to both Hennix’s writing and Flynt’s concept art, and as we shall see shortly, is implicit in Young’s notion of tuning as a function of time. Through the influence of Young, Hennix was predominantly concerned with just intonation intervals, i.e., intervals represented by ratios of whole numbers. As rational numbers can be individually enumerated and constructed in an intuitive manner, they would seem less in need of any conceptual revision or clarification than the classical continuum. Nevertheless, even under Brouwer’s construction they have somewhat different properties, in the sense that they remain a dynamic, infinitely proceeding structure rather than a completed set.

Under different foundational assumptions, for instance Esenin-Volpin’s ultrafinitism, even the natural number series loses its uniqueness and rigidity. This is a relevant example, as Hennix met Esenin-Volpin through the composer Maryanne Amacher in the early 1970s, and eventually became his student and collaborator. Esenin-Volpin’s conception of distinct natural number series became a significant component of Hennix’s work from the mid-1970s on. Many of her compositions, writings, and visual art reference Esenin-Volpin’s concept of “short infinitary processes,” and she considers different conceptions of a continuum of intervals once the natural number series has lost its uniqueness.

Interestingly, this notion of nonunique number series also arises in category theory. Any category having a “terminal object” has a so-called natural number object, which behaves similarly to the natural numbers. However, under sufficiently weak assumptions, these natural number objects may fail to be unique (i.e., there may be nonisomorphic natural number objects in the relevant category). In The Yellow Book, Hennix attempts to connect these categorical natural number objects to some of Wittgenstein’s remarks on the foundations of mathematics. She notes, “The logical object which corresponds to the natural numbers, ℕ, in the Tractatus, can be interpreted as a continuous variable set of natural numbers ℕ related to a topos construction satisfying the usual Kock-Lawvere axioms where the difference between two external natural number objects ℕ₁, ℕ₂ are interpreted as different stages of the construction of the internal natural number object ℕ₀.” 25

A topos under the standard Lawvere axioms has up to isomorphism a unique natural number object, so that must be the internal natural number object to which she refers. She claims that different “external” natural number objects can be interpreted as parts of a construction series for this “continuously variable set of natural numbers.” She does not make the exact correspondence to Wittgenstein’s philosophy of mathematics explicit; however, one can see her reflecting on the effects of removing the rigidity of the natural number series. Hennix later used this idea to theorize some of her compositions and visual art, in particular her Short Infinitary Process paintings.

From a more general compositional perspective, one can begin to detect a pattern in her work. If numbers model music, how does some foundational shift—for instance from classical to intuitionistic mathematics, or from constant structures to variable ones—influence the correspondence with musical intervals?

The most thorough analysis of this sort comes through Hennix’s engagement with Brouwer and her theorization of the music of Young. As detailed in my essay “Minimalism and Foundations,” facets of Young’s music bear a strong resemblance to Brouwer’s time and subject dependent version of mathematics.

For instance, several of his word scores in Compositions 1960 suggest potentially infinite constructions of the basic elements of music, geometry, and arithmetic, carried out through successive acts of introspection. Arabic Numeral (Any Integer) to H.F. (1960) describes a loud piano cluster to be repeated some given (but unspecified) number of times with as little variation as possible. This suggests a potentially infinite construction of a natural number series through the repetition of introspective acts, similar in spirit to Brouwer’s conception of a number series being a “repetition of ‘thing in time’ and ‘thing again.’” 26

Recall that for Brouwer, the basic “two-ity” is a sensation stored in memory as its passing away, being replaced by another sensation. In the special case of the empty “two-ity,” a self-same sensation of an empty cognitive state is replaced by another. Through its observation of self-similar events, Young’s Arabic Numeral resembles Brouwer’s construction of a two-ity, a three-ity, and so on. However, in this auditory version, the self-same act of introspection is based on the notion of listening to musical intervals. Later, Young and Hennix would specialize this to the case of rationally tuned intervals and their repeating composite waveforms. Along similar lines, Young’s Composition 1960 #7 gives a potentially infinite construction of one of the basic elements of music: it notates a perfect fifth to be held “for a long time.”

Perhaps most suggestive, Composition 1960 #10 to Bob Morris provides the instructions to “draw a straight line and follow it.” While this could be taken as a conceptual exercise, it reflects Young’s compositional process in that the piece is not only performed but carried out in a highly constructive manner. In the initial 1961 performances at Harvard (organized by Flynt, and realized by Young and Robert Morris) and at Yoko Ono’s loft, Young and Morris determined a sight, along with a point in the vicinity of where the line should end. Every few feet a plumb bob was aligned visually with the sight, with Young providing verbal directions on how to adjust the plumb. They made chalk markings on the floor, and later connected all markings with a yardstick. As in the process of tuning, the line was only built up over time through successive perceptual adjustment. While an elementary form was investigated, it was not treated as an external reality referred to by performance, but rather something constructed in time through the subject’s perspective.

In 1962, Young encountered just intonation, and from this point on the audible structure of the harmonic series became a central principle of organization in his music. The addition of tuning suggests an important theoretical refinement to Young’s approach: not only are structures of music potentially infinite, but so are the elements themselves. Comparing tuning to the astronomical observation of planets in orbit, he notes, “Tuning is a function of time. Since tuning an interval establishes the relationship of two frequencies in time, the degree of precision is proportional to the duration of the analysis, i.e. to the duration of tuning. Therefore, it is necessary to sustain the intervals for longer periods if higher standards of precision are to be achieved.” 27

Young goes on to argue that the accuracy of a tuned interval corresponds to the number of observed cycles of its periodic composite waveform. Instead of completed, “arithmetized” points on a continuum, intervals are given as constructions developing in time based on an idealized observer’s attention. Hence they resemble Brouwer’s choice sequences. Rather than idealized objects placed with infinite precision on a line, they are dynamic constructions requiring longer acts of attention for higher standards of precision. As Young notes, even in the simplest case of unison, it could take hundreds of years or more for one complete cycle of a composite waveform to occur (for frequencies sufficiently close together). As in Brouwer’s choice sequences, there is always a slight halo surrounding the status of an interval, given its essentially dynamic nature.

Furthermore, for irrational intervals there will never be even one complete cycle of a composite waveform. Young interprets this to mean that irrational intervals such as tritones are untunable. (Flynt constructed his Tritone Monochord [1987] as an objection to this claim.) Of course, under a classical interpretation, given any finite amount of time it is always possible to determine an explicit irrational number close enough to any given fraction such that one complete cycle of a composite waveform would take longer than the specified amount of time. Distinguishing between the two intervals would then take longer than that specified period of time, so it is not strictly possible to tell whether a rational or irrational interval has been performed. Indeed, this may have been part of the reasoning behind Hennix’s search for a new continuum of musical intervals. On the other hand, this statement only concerns Young’s theory of tuning. In practice, the just intonation intervals he engaged with were bounded by certain auditory principles, so with effort one could work out a suitably restricted version of the theory having the intended consequences.

Young’s principle is demonstrated in many of his compositions from the 1960s on. The Drift Studies of the late 1960s and ’70s involve rationally tuned sine tones gradually going in and out of phase over periods of observation. (It is worth noting that although Young refers to “tuning as a function of time” as one of his key theoretical constructs, the theory may have stemmed in part from technological limitations of the time, in particular the instability of commercially available oscillators in the 1960s.) Similarly, his Four Dreams of China of 1962 (and many later versions) involve sustained voicings of a single four-note chord and its subsets. One can see Young’s principle suggesting these pieces as further developments of potentially infinite constructions of musical intervals, rather than suspensions of completed forms.

Hennix met Young in New York in 1969, and in the same year Young commissioned her to realize one of his Drift Studies at the EMS studio in Stockholm. (EMS had recently acquired several phase-locked oscillators that allowed for much more stable versions of the Studies.) She also intended to realize a sine tone version of Young’s Trio for Strings (1958), although this project was never completed. Shortly after meeting Young, Hennix set out to write computer music for rationally tuned sine tones. Her method of composition is closely modeled after Young’s mid-1960s works, but she theorizes her approach more broadly, in terms of intuitionism, category theory, and set theory.

As noted above, Brouwer’s thinking overlaps with several tenets of the 1960s avant-garde. Most prominently, his mathematical systems are composed of acts of attention: a first sensation stored in memory at its passing away, being replaced by another sensation. This conception fits nicely within the framework of the post-Cage avant-garde, in which a composition is treated as a construction of mental states or located in the attitudes of the observer rather than existing as a completed, external state of affairs.

Through the influence of Cage, this notion became broadly prevalent. Although any number of examples could be chosen, the idea is perhaps most concisely expressed in an early word piece by the mathematician, composer, and Young collaborator Dennis Johnson: LISTEN (1960). It is easy to trace the influence of this idea on Hennix’s work via Cage, Flynt, and Young. Concept art sought a formalization of the construction of mental states common to works of the 1960s avant-garde. Flynt looked at the ambient aesthetic doctrine surrounding Cage’s work (most obviously 4'33'' [1952] but also his concept of indeterminacy) and sought to “apply new music to metamathematics.” 28 Similarly, Young’s focus on the audible structure of the harmonic series and other acoustical properties of sound emphasized the act of listening in the compositional process.

Given Cage’s influence on Young and Flynt, it is worth considering the kinds of mental states his compositions were supposed to bring about. While some think Cage’s use of chance operations was intended to generate novel compositions free from the obstructions of ego, it is perhaps most apt to characterize the newness or novelty of these compositions in terms of experiential states or mental attitudes, rather than externally defined states of affairs.

Echoing Lawvere’s remarks about constancy being the limiting case of variation, Cage notes, “If we think that things are being repeated, it is generally because we don’t pay attention to all the details. But if we pay attention as though looking through a microscope to all the details, we see that there is no such thing as repetition.” 29  Likewise, he writes, "New music: new listening. Not an attempt to understand something that is being said, for if something were being said, the sounds would be given the shape of words. Just an attention to the activity of sounds." 30

In fact, when Cage speaks of newness it is typically in relation to a certain kind of listening, which he refers to as a “purposeful purposelessness or a purposeless play. This play is an affirmation of life—not an attempt to bring order out of chaos.” 31 Of course, this disposition Cage describes is not itself new; the notion of a “purposefully purposeless” act of attention comes from Kant’s theory of aesthetic judgment, although Cage himself likely encountered it via Dewey. Compare Cage’s aforementioned statements to Kant’s Critique of Judgment: “Beauty is an object’s form of purposiveness insofar as it is perceived in the object without the presentation of a purpose.” 32  Kant writes,

 

The basis that determines a judgment of taste, can be nothing but the subjective purposiveness in the presentation of an object, without any purpose (whether objective or subjective), and hence the mere form of purposiveness, insofar as we are conscious of it, in the presentation by which an object is given us. . . . An aesthetic judgment refers to the presentation of the imagination, by which an object is given, solely to the subject; it brings to our notice no characteristic of the object, but only the purposive form in the way the presentational powers are determined in their engagement with the object. 33

Like works of Cage and Young, Kant’s judgment of aesthetic beauty does not reflect on the object presented but rather “the purposive form in the way the presentational powers are determined in their engagement with the object.” However, for Kant, judgments of beauty are not formed with respect to art (which he viewed as a secondary phenomenon) but rather to experiences of nature. For instance, in observing a flower one might enjoy perceiving an order to its structure. Yet upon further reflection we notice that this order exists nowhere outside of us, and what is actually experienced is “the presentation by which an object is given to us.” It is this mental state that underlies Cage’s compositional attitude, and the particular notion of “freeness” that Kant describes when encountering beauty will become important in a moment.

Via Cage, one can see a relation of concept art to more classical theories. Flynt’s “purely aesthetic proofs” explore the mind’s presentational powers, with the “syntax” of the language being a reflection on how objects are presented to us. Through Flynt, this formalization of the mind’s faculative powers becomes significant to Hennix.

One significant component of the cognitive freedom underlying Brouwer’s approach to mathematics was an experience of a play of the mind’s presentational powers. As noted above, this was also a central feature of Cage’s compositions, Young’s sustained compositions, and Flynt’s concept art.

Filtering this notion through the work of Lawvere, Hennix developed the idea of a topos representing a state of consciousness or modality of thought. It was noted earlier that “algebraic theories” can be represented by categories with finite limits, and that “algebraic theories of proofs” (i.e., λ-calculus) could be represented as Cartesian closed categories. Furthermore, these algebraic theories are purely syntactic objects, either presented or generated freely as strings of symbols. Following Flynt, Hennix associates such syntactic objects with mental acts or some display of the mind’s presentational powers.

Just as there are different modes in music expressing different emotional states, and in math different toposes corresponding to different “spaces to do mathematics,” Hennix links different toposes to alternative “places of thought” or states of awareness from which to perceive the world. She frequently refers to the Creative Subject as a free stream of sensations, and to a topos as some more structured state of awareness. One can see this view as an extension of Cage’s and Flynt’s work, permitting additional, more structured modalities of awareness by adding further specifications, analogous to different modes in music.

However, unlike Flynt, Hennix’s approach contains an explicitly stated semantic component. In category theory, a model of an algebraic theory is a functor from the appropriate category to the category Set (preserving some properties). While as a category, an “algebraic theory” (of which a topos is one particular instance) is a something like a “free” or “presented” object, a model for this category picks out a specific structure satisfying the conditions, or assigns a meaning to a collection of syntactic statements. Functors (or arrows) determine structure, a concept Hennix draws upon extensively in her work.

Following Lawvere, Hennix interprets a model as an arrow between categories. However, under her nonstandard interpretation of a topos, a functor realizes a state of consciousness or is an interpretation of mental states. Modifying the beginning of the Tractatus, she writes, “The world is formed of arrows. Each arrow is a fact—a mental fact. A mutual fact. . . . Philosophical problems can be analyzed as stacks of arrows.” 34

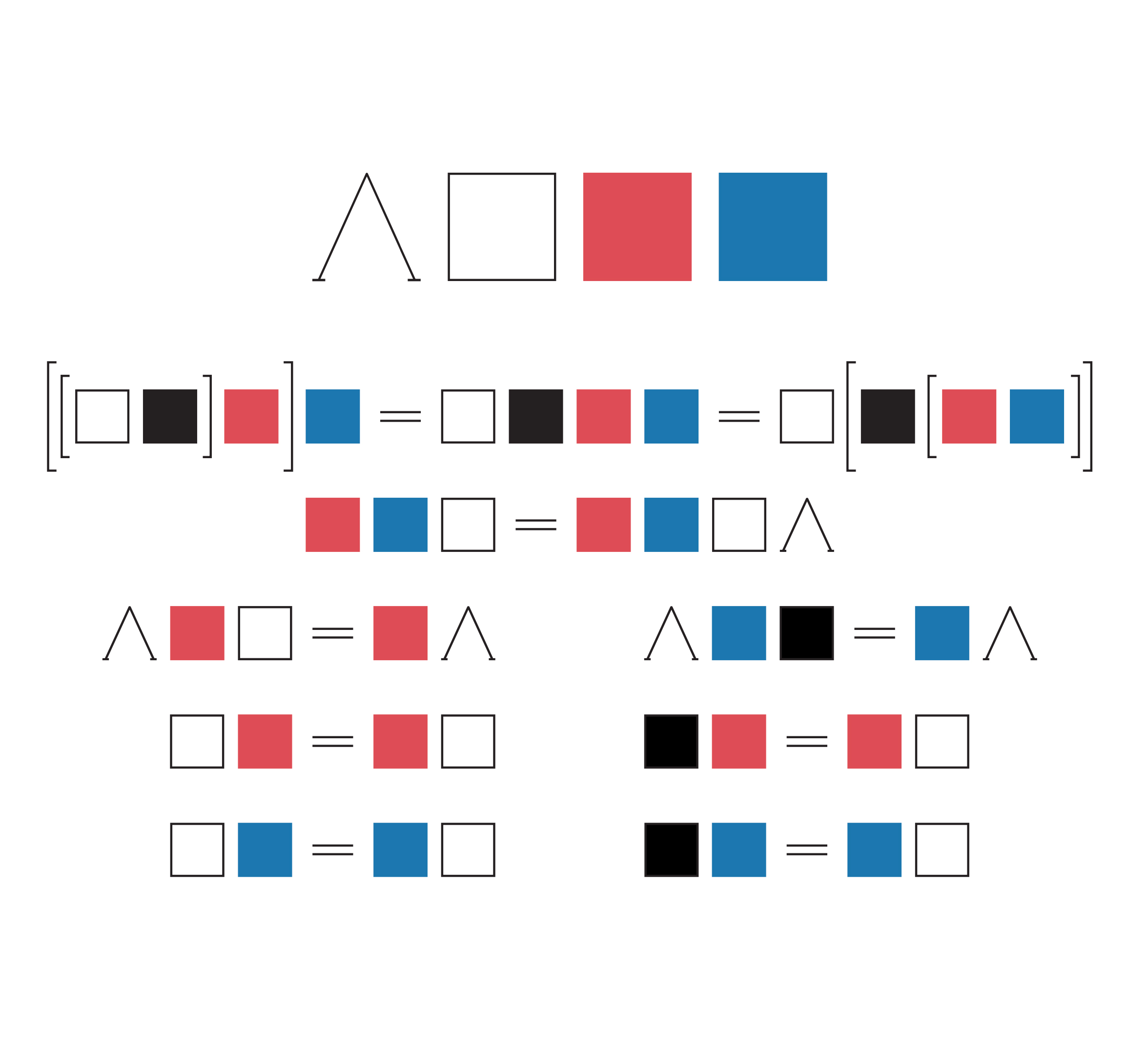
In response to Flynt’s concept art, in the mid-1970s Hennix developed her notion of Epistemic Art. These works involve “arrows” or interpretations out of spare syntactically presented objects. For instance, in the series Algebras w/ Domains (1973–91), red, blue, black, and white squares are painted on a grid, along with “equations” such as “a blue box followed by a white box equals a white box followed by a blue box” (she gives other, more complicated identities as well). The paintings are intended to specify “equational” or “algebraic theories.” One can see them as syntactic presentations of algebraic objects given as “free” objects (which are just strings of symbols, or in this case strings of colored boxes) modulo some relations that  allow for “word reduction.” (Of course it seems this string reduction will have to take place mentally.)

These syntactic objects can be interpreted on any structure meeting the requirements. In this case there is no “standard model,” and possibilities abound. Just as one interprets the theory of groups, or alternatively some string of symbols in a free group modulo some relations, on a specific group, one “interprets” the free or presented objects in the paintings on structures in the world. As we will see momentarily, her spare sine tone compositions function similarly, as “equational theories.”

Given the abundance of interpretations permitted, Hennix felt she had shifted the perspective on the “syntax rich, semantics poor” works of Flynt and Cage. Rather than a purely syntactic presentation of the mind’s presentational powers, Hennix added a substantive semantical component. Modifying Lawvere’s popular mantra from category theory, she contends that “our slogan has now become ‘Syntax poor, Semantics rich.’” 35 (Although one can see the syntax in both cases as fairly similar, Hennix formalizes her syntactic theory in the language of category theory and notes that models are appropriate arrows, as Lawvere did in his thesis.)

In 1976, there were two major presentations of Hennix’s work at Moderna Museet in Stockholm. The first was Brouwer’s Lattice, a weeklong concert series featuring several of her compositions, as well as a sound installation and pieces by Young and Terry Jennings. The second, a museum exhibition entitled Toposes and Adjoints (subtitled “A survey of abstract thought from Cantor to Lawvere”), featured texts, sculpture, sound installation, paintings, computer monitor displays, and incense, among other elements. A selection of titles gives a good indication of Hennix’s interests: Model for Set Theory ?, Open Point Set of Measure Zero, Brouwer’s Bar (Answering a question of Walter De Maria using Brouwer’s Bar Theorem), Short Infinitary Process, The Least Non-Measurable Cardinal, The Least Measurable Cardinal, Topos #1–14, among others. As in her writing, a loose and fully kaleidoscopic vision is evident, reminiscent of other 1960s-style world-building art.

Let us conclude with some remarks about these exhibitions. First, recall that a Brouwerian lattice is another term for a Heyting algebra, which expresses the internal logic of a topos. These toposes allow for generalized spaces of continuously variable structures, rather than just the special case of constant ones. Following Lawvere, Hennix chose this title as an expression of a move away from treating compositions as constant structures, and toward a more dynamic or synthetic approach, reflected in Young’s “algorithmic” compositions of the late 1960s and his notion of tuning as a function of time. In the notes to Brouwer’s Lattice, Hennix observes, “We owe the inauguration of this tradition,” which she terms Brouwer’s doctrine, “to La Monte Young and his fabulous New York City group of the 1960’s [sic]. . . . [One aspect of this approach is] a focus on evolving frames of musical structures rather than trying to obtain completeness. In this context completeness is misconceived.” 36

Hennix goes on to describe the theory behind her own computer-generated algorithmic infinitary compositions, expressed in terms of Brouwer’s notion of a choice sequence and Young’s algorithmic compositions. She writes, “The computer adds to the technical precision. You are never limited by physical exhaustion and there are no obstacles for proceeding with infinitely long spreads of musical events locked together by some appropriate algorithm that generates each new step on the basis of the preceding ones.” 37  Unfortunately, she never realized these choice sequence compositions, in part due to technical limitations of the time.

More generally, Hennix connects a Brouwerian lattice with a synthetic notion of space. In The Yellow Book, she writes:

Given a topos ? and an object X in ? . . . and any point p ∈ X the points well separated [i.e. of positive distance] from p are x ∈ ¬{p} while the points not well separated from p are the points x ∈ ¬¬{p} i.e. those points that are infinitesimally close to p. Since intuitionistically X = ¬¬{p} ∪ ¬{p} is false in general there must be some space unaccounted for in X. Remarkably this space is a “grey area” (a “no man’s land”) because it has no explicit description in the topos. 38

Here Hennix attempts to describe the role of a subobject classifier in a topos. Adopting a standard interpretation, she describes a topos as a kind of space, and a general Heyting algebra as a space with “grey areas,” where the union of a set and its complement may not comprise the entire space. While this example could be more precisely articulated in terms of an algebra of open sets, she connects the notion of “space” in a topos to Brouwer’s construction of the continuum, in which there is always a halo of “blurriness” as to where choice sequences are located. For instance, we have seen there are choice sequences x where x ≤ 0 or x > 0 is false. It is these “grey areas” that give Brouwer’s continuum its strong coherence properties, which Hennix chooses to express in terms of a non-Boolean Heyting algebra.

Several other pieces in Brouwer’s Lattice and Toposes and Adjoints are theorized in terms of Lawvere. For instance, the floor painting Open Point Set of Measure Zero (1976) contains black splotches on the ground in a random-looking pattern. Hennix writes that “different phases of the continuously variable sets are shown as a continuously variable floor painting. . . . Thus the floor painting serves simultaneously as both a picture and as a model for a finite set of topoi constructed in the style of F.W. Lawvere.” 39 Again, her use of Lawvere suggests a synthetic approach toward composition and visual art, expressed through cognitive structures.

The sound installation in Brouwer’s Lattice is Hennix’s infinitary composition from 1976, The N-Times Repeated Constant Event (sometimes written ◻^N). Following Young’s sine tone pieces of the late 1960s (and referencing his Arabic Numeral (Any Integer) to H.F.), the constant event is understood to be one complete cycle of a composite waveform of three rationally tuned sine tones.

While in Arabic Numeral integers are linked to Brouwer’s notion of time passing through direct experiential means, Hennix follows Brouwer in articulating a more primordial or idealized account of this procedure. Paraphrasing Brouwer’s “empty two-ity,” Hennix writes that the moment the subject comes to intuit the fundamental process of a waveform repeating in time “corresponds to a point in her life-world where a moment of life falls apart with one part retained as an image and stored by memory while the other part is retained as a continuum of new perceptions.” 40

Instead of realizing a two-ity, a three-ity, etc., through a repetition of self-similar piano clusters, Hennix interprets Brouwer’s basic mathematical system in terms of an observation of complete cycles of composite waveforms. Here Brouwer’s primordial intuition of time passing is directly tied to Young’s notion of tuning as function of time. In addition, Brouwer’s “empty two-ity” is now expressed in terms of the experience of “empty sounds,” in the sense that sine tones are waveforms divested of familiar qualities such as overtones.

Later in the Yellow Book, Hennix theorizes The N-Times Repeated Constant Event in slightly different terms. Since her theorization of the piece serves as a nice summary of the topics discussed in this essay, it seems a good way to conclude. In the following passage, she articulates three rationally tuned sine tones as presenting an equational theory (a collection of sine tones being representable in terms of trigonometric equations):

The triad ⟨x, y, z⟩ defines a class of equations E(x, y, z) which in turn determines a certain set of algebraic theories, Th(E) among which triples ⟨X, Y, Z⟩ and co-triples ⟨X^co, Y^co, Z^co⟩ have played an important role in my early formulations of an ALGEBRAIC AESTHETICS.

For each Creative Subject Σ who attends the space E′_◻ in which the composition ◻^N is developing freely, there exists a subjective time interval, τ*, during which the Creative Subject experiences a constant event ◻^*_⟨x,y,z⟩ as a subobject of the E′_◻-universally infinitely proceeding sequences of geometrically congruent composite waveforms ◻^τ_⟨x,y,z⟩.

In general the constancy of the subjective event ◻^*_⟨x,y,z⟩ can be experienced as fluctuating so that the subobject ◻^*_⟨x,y,z⟩ of E′_◻ (created by a Creative Subject’s attendance) as a submanifold ◻^N* of E′_◻  defines a continuously variable or discretely variable set (of (fluctuating) experiences of a temporal constancy of time). 40

This passage gives a good indication of both Hennix’s aims and the density of her texts, which often read like a private language or direct transcription of internal thoughts. While some notation is not defined and different concepts are blended together, one can sense a theory in the process of formation.

Like her Algebra w/ Domains paintings, the three sine tones are interpreted as spare syntactic objects yielding an “equational theory.” This syntactic theory of sound waves is “freely developing,” and can be observed by a Creative Subject in some given space E′_◻. Of course, since the sine tones are tuned in simple whole number ratios, the composite waveforms will repeat in self-same patterns. However, the specific standing wave pattern in the environment E′_◻ is determined by the space in which the composition is located, the speaker arrangement, humidity, etc. Hence the composition is not treated as a completed object but dependent on the specific surrounding environment.

Similarly, regardless of environmental complexity, the composition depends on an interpretation of this freely developing syntax. Hennix notes the Creative Subject may internally experience the composition as a subjective time interval in terms of its repeated waveforms. In practice this would occur very fast, but the observer’s experience may exist on a different time-scale than the waveforms themselves. As noted earlier, this experience can be described as a “point in her life-world where a moment of life falls apart with one part retained as an image and stored by memory while the other part is retained as a continuum of new perceptions,” or, in Brouwer’s terminology, an experience of an empty two-ity. Again, Hennix associates the experience of listening to sine tones with Brouwer’s spare cognitive act of constructing positive integers. Indeed, sine tones lack harmonics (and hence timbre), making them perceptually very difficult to locate. This lends them a feeling of sounds divested of familiar qualities.

However, as Hennix notes, this “repetition of thing in time and thing again” is a synthetic experience, which she ties to Lawvere’s philosophical remarks on the foundations of mathematics. She suggests we view E′_◻ as a “topos” created by the subjects’ acts of attention, and the subjective experience of ◻^*_⟨x,y,z⟩ as a subobject of an object in this category. The internal logic of this topos is intuitionistic, i.e., it is described by a Brouwerian lattice that is not Boolean. Hence, she views the objects in this category as continuously variable structures rather than constant ones. In this setting, she regards the “natural number object” of this category (as described above) as continuously varying or fluctuating experiences of the temporal constancy of time. In the composition, one directly experiences Lawvere’s remark about constancy being the limiting case of variation.